Where is Supersymmetry?
The original ideas
The original ideas for introducing supersymmetry dates back in the 1960s when, in the context of hadron physics that was found to be approximately spin-flavour independent, a symmetry between mesons and baryons was proposed.
These ideas, largely ignored at the time, found their way through mathematical investigations related to string theory into particle physics in the 70s, where, with the development of quantum field theory, a new symmetry — supersymmetry — relating bosons to fermions on the basis of a consistent algebra was developed. Andreas Hoecker (ATLAS experiment) notes: “A long way was crossed from the first theoretical concepts, developed in parallel on both sides of the iron curtain, to formulating the phenomenology of supersymmetry”. SUSY phenomenology and predictions for experimental observations came in the later 70s with the development of the minimal supersymmetric standard model (MSSM) and the concept of the so-called “R-parity” the conservation of which would avoid proton decay. The MSSM not only duplicated the number of known particles by introducing the supersymmetric partners of the Standard Model fermions and gauge bosons, but in addition required two Higgs doublets, leading to five elementary scalar bosons, and their corresponding SUSY partners.
The MSSM provided a number of favourable features that could cure shortcomings of the Standard Model — features that were not necessarily known to the fathers of supersymmetry. Paris Sphicas from the CMS experiment notes: “Years later, we know that SUSY can address three major issues in particle physics with a single strike of its magic wand: SUSY can “explain” how the Higgs boson can be so light (despite its being some 130 proton masses, its mass is many orders of magnitude smaller than what a straightforward expectation would dictate); it provides a great candidate for dark matter (in the form of the lightest supersymmetric particle); and lastly, it seems to hint that the interactions that we have been studying in particle physics (strong, weak and electromagnetism) might just be the manifestation of one unified ‘Grand Unified Theory’.”

A primary motivation for SUSY nowadays is its effect on the mass of the Higgs boson. One of the major weakness of the Standard Model is the presence of very large ‘radiative’ corrections to this mass. In the absence of any new physics, up to the largest energy scales where gravity would come into play, these corrections are much, much larger than the mass of the Higgs boson itself. And this makes difficult to explain the observed mass of 125 GeV. A new mechanism — e.g. a new symmetry — can lead to a natural cancellation of these radiative corrections. SUSY achieves just that.
Another strong motivation for SUSY comes from the observation that the electroweak and strong coupling strengths seem to evolve towards each other with rising energy. Nevertheless, they do not quite meet at a single value, which would be the sign of ‘grand unification’ of the Standard Model forces. Such grand unification would not only be a beautiful generalisation of the Standard Model, but would also allow protons to decay, a property deemed necessary to generate the observed excess of baryons over anti-baryons in the universe. If SUSY materializes at energy scales of 1 TeV or so, it would modify the evolution of the couplings such that grand unification might be realised. And even more: the energy scale at which unification would occur would likely be large enough to push the lifetime of the proton beyond current experimental limits.
Finally, the third argument in favour of SUSY is that, under certain circumstances, it offers a mechanism that could explain the observed dark matter in the universe. If “R-parity” and thus the number of SUSY particles is conserved (i.e. they are only produced by Standard Model processes in pairs) then the lightest SUSY particle (LSP) could not decay to solely Standard Model particles; it would thus be stable. If this LSP is neutral and weakly interacting, it is a perfect candidate for dark matter: it could even match the required amount of dark matter that has recently been precisely determined from the data of the Planck satellite.
Image Credit: Particle Fever film
There remains but one question: what is the manifestation of the existence of SUSY in nature? The answer is striking: every particle of the Standard Model (SM) would have a supersymmetric analog or ‘partner’, which would be identical to the SM particle, except for its spin. Quarks, which have spin 1/2 would have scalar (spin 0) partners, called ‘squarks’; leptons would follow suit: they would have spin-0 partners called ‘sleptons’. The situation would be almost the same for the carriers of force; there is a technical difference with respect to quark and lepton partners, in that the physical SUSY partners of the SM bosons would be admixtures of states that include the Higgs SUSY partners.
If supersymmetry were an exact symmetry, the mass of each Standard Model particle and its SUSY partner would be equal. Nature, of course tells us otherwise: there is no scalar (spin 0) particle as light as the electron, while also no other superpartners have been seen so far. Paris Sphicas explains: “This is where one has to introduce additional concepts, e.g. ‘breaking’ supersymmetry so as to make these partners much heavier than the standard model particles. There are several ways of doing this, and thus, one ends up with different ‘variants’ of SUSY. Having said this, even within any specific variant, there are still several unknowns, with the most important one being the precise mass spectrum of all the SUSY particles.” This is very important, because this spectrum governs the experimental signatures that would result from the presence of these SUSY particles. As an example, if A is heavier than B, then A can decay to other particles and B. And this is a totally different scenario than B being of higher mass than A. Another example is offered by the lifetimes: if A is short-lived we expect one set of signatures, which are very different from when it is long-lived (and in some case not decay even within the large LHC experiments).
Experimental collider searches for SUSY…
The hunt for SUSY has been ongoing since the 1980s, at the SPS proton–antiproton collider (with the UA1 and UA2 experiments), and the e+e– colliders PEP (SLAC, USA), PETRA (DESY, Germany) and Tristan (KEK, Japan). This was followed by an extensive set of searches at LEP and the Tevatron up until the LHC started operation. Strong indirect limits on SUSY came from flavour physics measurements as performed, among others, at CERN by the NA48 experiment and at the SLAC and KEK B-factories. Also the non-observation of an electric dipole moment in the neutron or in atoms and precise measurements of the anomalous magnetic moment of the muon constrained SUSY models. However, the flexibility offered by the unknown breaking mechanism allowed to tune SUSY such as to evade these constraints and still allow relatively light SUSY particles that could be produced by the LHC. Andreas Hoecker notes: “Throughout this period, and during the LHC data taking phase, the experimental searches for SUSY particles have evolved significantly”. In broad terms, one set of searches is relevant when we insist that SUSY provides a dark matter candidate. The latter being weakly interacting should escape the LHC detectors and should create a measureable momentum imbalance in the event transverse to the beam axis, much like neutrinos from decays of the W and Z bosons do. This is the famous "missing transverse momentum" signature, which has been the telltale signature of SUSY searches since the SPS. The other set of searches gives up on solving "three problems for the price of one" and allows R-parity to be broken, so that the lightest SUSY particle can decay to Standard Model particles. These searches can be more difficult, as the background from the Standard Model may be very large (as an example, the production rate for quarks is much larger than the one for squarks, since the latter are assumed to have much larger mass and have spin 0). Paris Sphicas explains: “Today, we have explored large parts of SUSY ‘parameter space’. The large centre-of-mass energy at the LHC has made the ATLAS and CMS experiments sensitive to sparticle masses that are well beyond the direct limits obtained at earlier hadron colliders. The results on electroweak SUSY production from LEP are however harder to crack. With the increasing luminosity, however, even those are giving way to the LHC results. In simple terms: we have been looking for SUSY in several scenarios, and have not found it. To quantify this null result, we calculate ‘limits’ on the SUSY particles.”]
The most typical R-parity conserving models of SUSY would predict signatures with jets and missing transverse momentum at the LHC, where the jets originate from decays of pairs of squarks or gluinos, the SUSY partners of quarks and gluons, and the missing transverse momentum stems from the undetected weakly interacting lightest SUSY particles (LSP). Searches for such events have not revealed any signal and provide the strongest bounds excluding gluino masses up to 1.8 TeV depending on the details of the SUSY model assumed. Sphicas adds: “This is an example of a ‘lower limit’ on the mass. The large majority of the limits we obtain are of this type. And what is the result? Well, we conclude that the SUSY partners must have masses larger than the limits determined by the analysis.” These limits, however, are not absolute but depend on other characteristics of SUSY. As Hoecker points out: “For example, large LSP masses reduce the available phase space for missing transverse momentum in SUSY events, which deteriorates the sensitivity of the searches.”
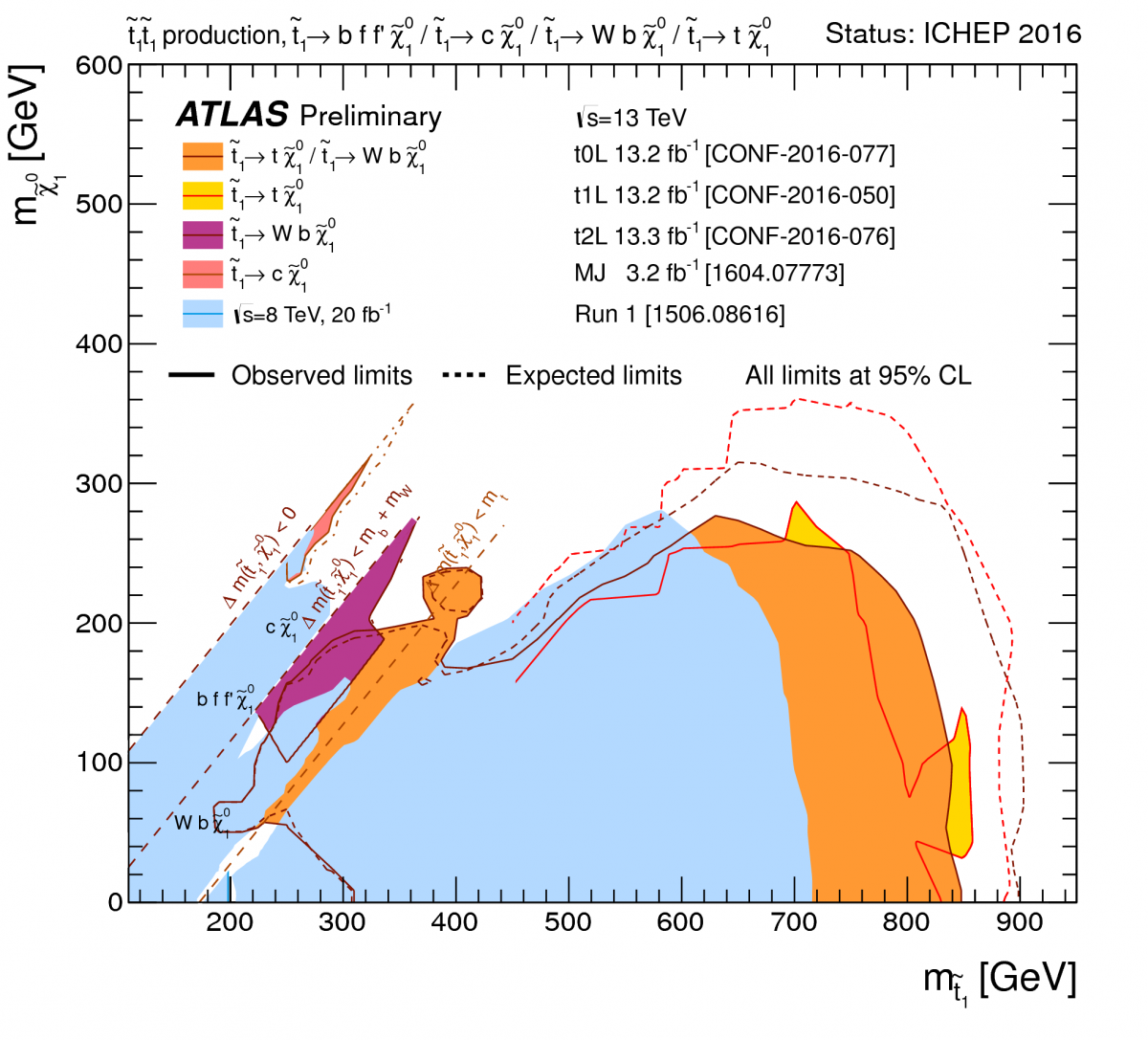

Summary of the dedicated ATLAS searches for top squark (stop) pair production (top figure) and CMS EWKino searches (bottom figure) based on pp collision data taken at √s = 13 TeV during Run 2 of the LHC.
If one wants to tackle natural SUSY, which describes a flavour of SUSY that allows to moderate the hierarchy problem by cancelling the Higgs radiative corrections, one needs to search for light top-quark partners (top squarks, also denoted stop). Stop pair production has similar final states as top pair production with, however, additional missing transverse momentum from the two escaping LSPs but also much lower cross section (roughly six times lower if the stop had the same mass as the top quark). Highly optimised analyses searched for direct and gluino mediated stop pair production in all kinds of decay scenarios. These analyses have allowed the exclusion of stop masses of up to 900 GeV (for low-mass LSPs).
It might also occur that strongly produced SUSY particles are too heavy for the current reach of the LHC and only electroweak SUSY particles are produced. Their signatures would resemble Standard Model multi-boson production giving final states with two or more leptons, only a few jets, and missing transverse momentum. Again, ATLAS and CMS have been looking for such events in highly optimised dedicated searches with, so far, no success.
The lack of evidence has inspired the experiments to also search for SUSY in events with long-lived particles or relaxed of R-parity conservation requirement. Long-lived heavy particles are predicted in many new physics models, not only SUSY. Hoecker explains “Long-lived particles may occur if new particles can only decay through much heavier intermediate states (such as predicted in a SUSY flavour called split supersymmetry), in case of a small coupling strength (such as predicted in some gauge mediated SUSY breaking scenarios where the gravitino is the lightest SUSY particle), or if there is mass degeneracy in a cascade decay (as is present in some SUSY breaking scenarios).” The search for long-lived particles employs very interesting features of the detectors such as specific ionisation loss and time-of-flight measurements, or the reconstruction of highly displaced decay vertices, and usually requires dedicated reconstruction. Searches for R-parity violating signatures approach those for non-SUSY new phenomena such as hunts for bumps from resonances or events with many leptons or many jets, but no missing transverse momentum as the lightest SUSY particles are allowed to decay to Standard Model particles.
It is clear that, beyond its intrinsic fascination, SUSY is also a powerful tool to generate new physics models for the LHC searches. Andreas Hoecker notes: “if we see a signal in one of our SUSY searches, many additional measurements would be needed before a statement about the nature of the signal could be made.”
Lessons and next steps…
The way in which experiments search for SUSY may have changed but the motivation has stayed the same, namely, finding a solution to the hierarchy problem, to force unification and dark matter. Andreas Hoecker points out that today we have an additional reason that is the Higgs discovery at 125 GeV: “The fact there seems to be only one elementary scalar particle, the Higgs boson, and that it is light is peculiar and something that needs further exploration.”
As mentioned above, the way SUSY is probed at the LHC has evolved compared to previous experiments. Full ‘top-down’ models of SUSY that predict, based on a few but strong assumptions on the hidden SUSY–breaking sector, the entire SUSY particle spectrum and hence the experimental signatures, have mostly been replaced by so-called simplified models that take a more ‘bottoms-up’ perspective. Single SUSY processes are systematically explored in terms of the masses and mixing properties of the SUSY particles occurring in them. This allows the development of signature-based search strategies that, taken as an ensemble of many searches based on different simplified models, have been shown to adequately cover also full SUSY models. As Andreas Hoecker notes: “Simplified models are an extremely useful tool for experimentalists. They allow us to efficiently address particular features of SUSY such as stop/sbottom production, electroweak production, compressed spectra, massive long-lived particles, R-parity violation, etc. without the need to embed these in a complete SUSY model.” The term “compressed spectra” defines a particularly difficult, but theoretically well possible SUSY parameter scenario in which the produced SUSY particles have small mass differences. The consequence of such a configuration would be softer particle spectra and less missing transverse momentum. Searches for SUSY with compressed spectra need large data samples and will greatly benefit from the high-luminosity upgrade of the LHC.
There has been a tremendous effort in trying to understand whether there are loopholes in the searches, that is, whether there are regions of parameter space (i.e. of mass values of the SUSY particles) that are below the experimental limits and yet would have escaped the searches. Such scenarios have been narrowed down with the increasing data statistics and ever-improving understanding of detectors and Standard Model processes.
If by the end of the LHC programme no evidence for SUSY is seen would be a disappointment for many particle physicists. For Sphicas: “In some sense, it would be a great opportunity that nature decided not to take advantage of. Presumably, because she found an even better opportunity.”
For Hoecker: “The exclusion limits on SUSY and other new physics scenarios obtained at the LHC continue to put stress on the naturalness of the scalar sector of the Standard Model. However, although naturalness, that is the factorisation of very different distance scales, is appealing and a central concept in physics, we do not know whether Nature obeys to it for the Higgs boson. The experiments need higher luminosity and eventually higher energy to progress on this profound question.”
HL-LHC upgrade and plans for a future high-energy circular collider…
Searches for SUSY will benefit from the HL-LHC upgrade and, furthermore from a future high-energy hadron collider. Roughly, a 100 TeV collider would allow the experiments to probe SUSY particles that are ten times heavier than the LHC is currently sensitive to.
At some point in time, we will be close to the ultimate masses that the LHC can explore, and the question will become what happens next. Sphicas explains: “When we do reach that stage, the answer is simple: we will have to go higher in the masses we probe; and up to now, this has meant increasing the energy of our machines. Perhaps an example from history can help here: with the u, d and s quarks discovered, there was a solid and quite predictive theory of particles and their interactions. And in terms of ‘observables’, essentially the only measurement that did not quite fit in was some rare decays of neutral kaons. The solution to that was proposed by Glashow, Iliopoulos and Maiani (the so-called GIM mechanism). It was an elegant solution, but it demanded the presence of a fourth quark. Theory provided guidance that ‘something must happen by ~2 GeV’. And the tilde implies a rough approximation. Thankfully, the experiments at Brookhaven (S.C.C.Ting) and SLAC (B.Richter) had enough energy to produce the J/psi, the bound state of this new quark and its antiquark. The discovery is known as ‘the November revolution’ – for a revolution it was. What would have happened if the available accelerators did not have enough energy to produce these particles? I guess the next step would be to build one that could!”
So you may wonder will we ever know with certainty if SUSY exists or not? “Yes, the day we discover it!” answers Sphicas. As for the other case: just like we will never know that the proton does not decay (all we can ever show is that it decays more slowly than some incredibly small rate), it is impossible to show that something does not occur in nature.
As to whether there are alternatives to SUSY? Here is a quick answer from Sphicas: “Of course there are alternative theories that try to tackle the same questions. Human imagination and more specifically the creativity of theorists have been shown to be boundless. The one thing that can be said about SUSY is that it seems to be the only one that could solve three issues for the price of one new principle. Of course, the stress here is on the words ‘seems to be’”.
The author would like to thank Andreas Hoecker (ATLAS) and Paris Sphicas (CMS) for their invaluable contribution and thoughtful comments on this article.
Latest public results for SUSY searches in the dedicated pages from the ATLAS (here) and CMS (here) experiments.
