In April 2024, the Dark Energy Spectroscopic Instrument (DESI) collaboration released their first cosmological results [1]. These results made the news primarily because they showed some hints of dynamical dark energy (see the article in the same issue of the EP newsletter). However, they also had key implications for neutrinos. Neutrinos were produced in huge numbers after the Big Bang, and they always represent a relevant component of the energy density of the Universe. DESI data, in combination with the exquisite Cosmic Microwave Background (CMB) observations from Planck, were used to set a constraint on the sum of the neutrino masses of Σm_ν < 0.073 eV at a 95% confidence level (CL). This result is surprising because we know from laboratory experiments that at least Σm_ν > 0.06 eV, and we would have thus expected to see the first hints of a signal. These results from DESI are clearly intriguing and have important implications for fundamental particle physics. In this article, we delve into this, and in particular, we will answer the following questions: Why is cosmology sensitive to the neutrino mass? What did DESI measure, and how are these measurements used to constrain the neutrino mass? What do we know about neutrino masses from the laboratory? And why could it be that the DESI bound on Σm_ν is so strong?

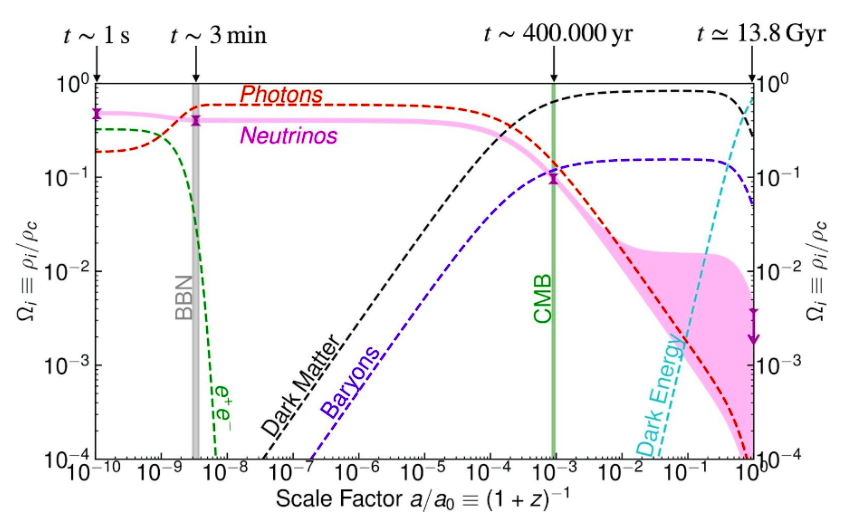
Figure 1. Evolution of the fractional contribution to the energy density of the Universe from various of its components. The x-axis represents the scale factor, i.e., how much the Universe has expanded. On the upper x-axis, the age of the Universe is shown for illustration. The key players for this article are the neutrinos highlighted in magenta. The width of the band roughly corresponds to the current uncertainty we have from cosmological observations. We can clearly see that neutrinos are always a relevant component of the energy density of the Universe throughout its entire history. Credits: Miguel Escudero Abenza, see [2].

Why is cosmological data sensitive to the neutrino mass?

Neutrinos were produced in large abundance after the Big Bang, and when the Universe was only ~1 second old, it was cool enough (T~MeV) that they stopped interacting with anything. At this point, the Cosmic Neutrino Background was formed. As highlighted in Figure 1, within the standard cosmological model, neutrinos always represent a relevant component of the energy density of the Universe. In particular, we expect that today there should be about 300 neutrinos per cm³. This may seem like a very small number if we compare it with the typical densities of materials on Earth. However, what is key is that there are about 300 neutrinos in every cm³ of the Universe, and since they are massive, represent a non-negligible component of the energy density of the Universe (ρ_ν = m_ν x n_ν).

Their main impact is to: 1) modify both the expansion rate of the Universe because, within General Relativity, the expansion rate is proportional to √ρ, and 2) reduce the speed at which structures (galaxies and clusters of galaxies) grow. Neutrinos behave as non-cold dark matter because they only interact gravitationally, but unlike cold dark matter, they have a non-negligible velocity because they were still relativistic when they were produced. Since they travel at relativistic speeds, unlike cold dark matter, they cannot get trapped in gravitational potentials. Therefore, the larger their energy density, the harder it is to form structures in the Universe (since neutrinos do not fall into these potentials). These two effects are directly proportional to the energy density in neutrinos and, therefore, their mass, resulting in: 1) an enhanced expansion rate of the Universe, and 2) a decrease in the rate of formation of large-scale structures.

What did DESI measure, and how are these measurements used to constrain the neutrino mass?

Currently, the best handle on the cosmological effects of the neutrino mass comes from Planck CMB observations. The CMB is sensitive to these effects because the enhanced expansion history driven by a larger neutrino mass directly impacts the distance at which the CMB was formed, and the decrease in structure growth affects the propagation of CMB photons from when they were produced until today. From these effects, and within the standard cosmological model, the Planck collaboration reports that Σm_ν < 0.24 eV at 95% CL [4].

How does DESI data help in this regard? DESI measured the positions of about 5 million galaxies and 1.5 million quasars (active galaxies) in the sky. These measurements are key because these positions give us a picture of how the Universe evolved over the past 10 billion years. The feature extracted from DESI data was Baryon Acoustic Oscillations (BAO), a direct analogy to the CMB acoustic peaks but shown by galaxies themselves. This BAO feature, as a function of redshift, is then used to constrain parameters that influence CMB anisotropies, such as total matter abundance and the Hubble constant. This enhances Planck data's ability to limit or measure the neutrino mass. Combined, the CMB+DESI-Y1 bound is Σm_ν < 0.073 eV at 95% CL.

What do we know about neutrino masses from the laboratory?

There is currently no problem with a bound on Σm_ν < 0.073 eV at 95% CL. A combination of neutrino oscillation experiments has accurately measured the mass-squared differences of the three active neutrinos [5]. At present, however, we do not know whether the lightest neutrino has the most mixing with νe (normal ordering, NO) or with the least mixing (inverted ordering, IO). Depending on this, we know that the sum of neutrino masses is bound to be Σm_ν > 0.06 eV (NO) or Σmν > 0.10 eV (IO) at 5σ CL.

Why could it be that the DESI+CMB bound on Σm_ν is so strong, and yet there is no evidence for it? This is the million-dollar question, and there are three potential answers: 1) a result of a systematic effect in either DESI or Planck data, 2) a statistical fluctuation in either data set, or 3) a potential sign of deviations from the standard cosmological model. All of these possibilities have been recently thoroughly analyzed in [8], and we discuss them here. Options 1) and 2) – DESI measures the position of galaxies that were already measured by previous galaxy surveys, in particular, by the Sloan Digital Sky Survey (SDSS). The averaged distance measurements as a function of redshift are highlighted in Figure 2.

Figure 2. Angular diameter distance (left) and Hubble rate (right) as a function of redshift as measured by various galaxy surveys (BOSS, SDSSS, and DESI), as well as the 1σ and 2σ prediction from Planck (gray contours). One can see rather good agreement between the prediction and the measurements but for the data point at z = 0.7 on the left from DESI LRG2 (Large Red Luminous galaxies) as well as the data point at z = 0.5 on the right (LRG2). Credits: George Efstathiou [9].

From this figure, we can clearly see that the DESI data points broadly agree with previous SDSS measurements as well as with the Planck predictions, but there are a ~2-3σ outliers at z = 0.5 and 0.7. This distance is made from luminous red galaxies (LRG), which have been observed for decades now with previous instruments. Statistically, assuming Gaussian statistics, the probability of randomly obtaining such an outlier is about 1.8% [9], so nothing particularly worrisome. It was shown [8] that the data point at z = 0.7 does significantly push downwards the inference for the matter abundance in the Universe. This, in turn, leads to a neutrino mass bound that is weaker by 30%, thus leaving it somewhere around Σm_ν < 0.093 eV at 95% CL. It remains to be seen in future data releases if this was just a statistical fluctuation or a real trend in the data, but it does have an impact on the neutrino mass inference.

Could there be systematics in Planck CMB data?

Planck CMB data is the most powerful cosmological data set to date and has allowed sub-percent precision determination of various cosmological parameters. However, CMB data reconstruction requires disentangling the primordial CMB fluctuation signal from other emissions such as dust or synchrotron radiation from the galaxy. In this context, in the legacy Planck 2018 analysis, the so-called lensing anomaly was reported, which meant that somehow, the power spectrum of CMB anisotropies was sharper than one would have expected. This is precisely the same effect that the neutrino mass produces in the CMB spectra. Importantly, there have been new reanalyses of Planck data that count with slightly higher statistics but critically with a better handle on these systematic effects. They now do not report any sign of this anomaly and this gives even further confidence in the neutrino mass bounds. However, the neutrino mass bound does change upon the Planck likelihood implementation used in the analysis and this is reflected in Figure 3. There one can see that using the old Planck 2018 or using the new (2023) likelihood implementation does lead to relevant changes in the neutrino mass limit (compare black and red). If one further adds the effect of the DESI-Y1 outliers the bound can be relaxed by almost a factor of 2, although it seems complicated to weaken it beyond 0.11 eV within the standard cosmological model.

Figure 3. Frequentist analysis of the cosmological neutrino mass bound using various cosmological data sets under the assumption of the standard cosmological model. The reference bound is shown in black, but it should be compared with the red one (newer Planck data), as well as the green one (no DESI-Y1 z=0.7 bin). One can clearly see a relevant relaxation of the bound in those cases. The contours are extrapolated to the negative regime (unphysical) to see if data supports a preference for a “negative” neutrino mass. Credits: Daniel Naredo-Tuero [8].

Beyond the standard cosmological model, there are several scenarios that could relax the cosmological neutrino mass bound. One of them is precisely dynamical dark energy (which DESI data seems to support to some degree). If one allows the equation of state of dark energy to vary (in combination with the neutrino mass), then the bounds will be relaxed up to 0.2 eV at 95% CL, still leaving a factor of 2-4 compared to the minimum allowed by neutrino oscillation experiments but still substantially stronger than the current laboratory limit by the KATRIN experiment: Σm_ν < 1.35 eV at 90% CL [3]. There are other cosmological scenarios where the cosmological neutrino mass bound could be relaxed or fully evaded, some of which are connected to relevant particle physics models. These include neutrino decay, long-range neutrino interactions, and late-phase transitions. The motivation for these kinds of scenarios is currently weak, but if future cosmological missions do not detect the neutrino mass, we could well be seeing the first hint of a non-standard neutrino property.

Summary: where are we and where are we heading towards?

To summarize, the release of DESI-Y1 data marks the starting point of an unprecedented precision era in cosmology. Using existing CMB data in combination with DESI-Y1-BAO measurements, the DESI collaboration reported a bound on the sum of neutrino masses of Σm_ν < 0.073 eV at 95% CL. This bound is very strong as it is very close to the minimum possible value of the sum of neutrino masses we know from the laboratory: Σm_ν > 0.06 eV (NO) or Σm_ν > 0.10 eV (IO) at 5σ CL. In particular, it would disfavour already the IO hypothesis. How robust is this bound? First, it depends to some extent on the Planck data set used to analyze it, and it can be weakened by 30-40% as a result. Second, there are some outliers in DESI-Y1 data which pull the bound significantly towards smaller masses. It would be interesting to see if this trend is confirmed in future data releases. When both effects are taken into account, the bound weakens to Σm_ν < 0.11 eV at 95%CL and, therefore, still compatible with both NO and IO. Third, it depends upon the assumed cosmological model. For instance, if one allows for further effects beyond the standard cosmological model, such as a time-varying equation of state of dark energy, the bound degrades to Σm_ν < 0.2 eV at 95%CL. It is important to emphasize that, as of today, no cosmological data set has any indications for a non-zero neutrino mass in cosmology.

The upcoming future on this matter looks particularly bright. DESI has already collected 3 times more data than for Y1, and the European Euclid satellite (which will collect the positions of even more galaxies) is fully operational and will start collecting cosmological data very soon. We expect detection of the neutrino mass from a combination of DESI, Euclid, and CMB experiments within 5-10 years. If, given unprecedentedly small statistical and systematic errors, no detection is made, this would be a call for physics beyond the standard model of cosmology and particle physics, possibly signalling a new unidentified property of neutrinos (such as their decay). Either way, the upcoming years are going to be extremely exciting for neutrino cosmology.

References

[1] DESI Collaboration, DESI 2024 VI: Cosmological Constraints from the Measurements of Baryon Acoustic Oscillations, https://arxiv.org/abs/2404.03002 

[2] M. Escudero Abenza, Modern Neutrino Cosmology, CERN-TH Colloquium, March 13, 2024, https://indico.cern.ch/event/1385110/.

[3] KATRIN Collaboration, Direct neutrino-mass measurement based on 259 days of KATRIN data, https://arxiv.org/abs/2406.13516. 

[4] Planck Collaboration, Planck 2018 results. VI. Cosmological parameters, A&A 641, A6 (2020), https://arxiv.org/abs/1807.06209. 

[5] S. Navas et al. (Particle Data Group), Phys. Rev. D 110, 030001 (2024). https://journals.aps.org/prd/abstract/10.1103/PhysRevD.110.030001

[6] W. Yifang, Status and Prospects of the JUNO neutrino experiment, CERN Colloquium March 20, 2024, https://indico.cern.ch/event/1371187/

[7] NUFIT, http://www.nu-fit.org/ 

[8] D. Naredo-Tuero, M. Escudero, E. Fernández-Martínez, X. Marcano, V. Poulin, Living at the Edge: A Critical Look at the Cosmological Neutrino Mass Bound, https://arxiv.org/abs/2407.13831 

[9] G. Efstathiou, Challenges to the ΛCDM Cosmology, Phil. Trans Roy. Soc. A (2024), https://arxiv.org/abs/2406.12106