In discussion with Cumrun Vafa

In the realm of theoretical physics, few minds are as celebrated as Cumrun Vafa. Cumrun Vafa is the Hollis Professor of Mathematicks and Natural Philosophy in the Physics Department at Harvard University. Throughout his career, he has made groundbreaking contributions to our understanding of the universe, from the nature of space and time to the intricacies of black holes. We engage with Professor Vafa in a conversation that delves into the complexities of theoretical physics, the challenges, and opportunities it presents, and the advice he has for aspiring physicists embarking on their journeys of discovery.
What ignited your interest in this field, and how did your family and teachers contribute to nurturing it?
Cumrun Vafa: My journey into physics began with a simple fascination for the power of mathematics to explain real-world phenomena. It all started when a cousin introduced me to the idea that simple mathematical calculations on paper could actually predict outcomes in the physical world. My fascination with science likely began as early as second grade. I vividly recall gazing at the moon and pondering, "Why doesn't it fall? What keeps it suspended in the sky?" By third grade, I had grasped the concept of objects possessing length, height, and width. This sparked a new question: "Why are there specifically three dimensions associated with objects? Why not more, or fewer?" This early curiosity foreshadowed my later understanding of why we inhabit a three-dimensional world. This revelation left a profound impression on me, sparking a curiosity that would shape my entire life. Additionally, my family played a pivotal role in fostering this curiosity. They encouraged my exploration of the natural world from a young age, allowing me to ask questions and seek answers freely. Their support gave me the foundation I needed to pursue a career in physics.
It's fascinating how early experiences can shape our future paths. You've mentioned that one of the things that puzzled you as a child was the lack of questioning about our world? Is this also an attitude that you encountered later during your graduate studies?
Cumrun Vafa: Throughout my career, I've observed a tendency within the scientific community to accept conventional wisdom without questioning it deeply enough. I understand that this is also a matter of taste and it appears that my taste is sometimes very different from that of other communities within our field. Personally, I've always been driven by a curiosity to explore the unknown and challenge existing paradigms. I believe that scientific advancement thrives on diversity of thought and a willingness to question the status quo. That's why I value collaboration with colleagues who bring different perspectives to the table. By engaging in open dialogue and debate, we can push the boundaries of knowledge and uncover new insights together.
Your contributions to theoretical physics, particularly in the realm of string theory, have been groundbreaking. What initially drew you to this area, and what keeps you motivated to delve deeper into its complexities?
Cumrun Vafa: String theory captured my imagination from the moment I first encountered it. The idea that tiny, vibrating strings could be the fundamental building blocks of the universe seemed both elegant and profound. What drew me in was the potential of string theory to provide a unified framework for understanding the fundamental forces of nature, including gravity. This grand vision continues to motivate me to explore the mysteries of string theory further. With each discovery and breakthrough, I'm inspired to uncover more about the underlying structure of reality and the nature of the cosmos.
Your academic journey has been rich and diverse. Could you shed some light on how your early work, such as your Ph.D. thesis, laid the groundwork for your later exploration of string theory?
Cumrun Vafa: Absolutely. My PhD thesis centered on the unbreakability of certain symmetries, like parity in QCD. I explored this concept theoretically and investigated related ideas. In essence, my thesis focused on symmetries and quantum field theories. While I had already begun working on string theory at the time, I chose to dedicate my thesis to the research that occupied the majority of my graduate studies. While my Ph.D. thesis focused on a different aspect of theoretical physics, namely the stability of symmetries in quantum field theories, it provided me with valuable insights and skills that would prove instrumental in my later work on string theory. The rigorous training I received during my doctoral studies equipped me with the analytical tools and mathematical prowess necessary to tackle the complexities of string theory. Moreover, it instilled in me a deep appreciation for the underlying symmetries and structures that govern the laws of physics, which are central to both quantum field theory and string theory.

In 2017, Vafa, alongside Andrew Strominger and Joseph Polchinski, jointly won the Breakthrough Prize in Fundamental Physics for their advancement of string theory and jointly won the 2014 Breakthrough Prize in Physics Frontiers Prize. Vafa is also the recipient of the Abdus Salam International Centre for Theoretical Physics (ICTP)'s, 2008 Dirac Medal, which was won alongside Juan Maldacena, and Joseph Polchinski for their advancement of string theory. In January 2014, Vafa has received one of the prestigious Humboldt Research Awards Credits: Photograph by Brigitte Lacombe/Breakthrough Foundation.
While quantum theory forms the cornerstone of our understanding of particle physics, key questions remain unanswered, such as the hierarchy problem and the nature of electroweak symmetry breaking. How are researchers making progress in addressing these challenges, and what are the implications of these advancements for our understanding of particle physics?
Cumrun Vafa: Quantum field theories (QFTs) act like a recipe, where you specify the ingredients (fields) and desired properties (symmetries) to cook up the most general system possible. Surprisingly, this often results in very few adjustable parameters, which can be set to some natural values.
However, exceptions exist. The electroweak hierarchy problem and the cosmological constant are prime examples. Various approaches have been taken to address these issues. For instance, supersymmetry aimed to explain the electroweak hierarchy's stability. It proposed the existence of a new layer of particles mirroring the known ones, aiming to explain the electroweak hierarchy's stability. However, recent data from the Large Hadron Collider (LHC) suggests it might not be the answer.
Traditionally, gravity has been left out of these discussions. The prevailing thought was that its influence becomes negligible at larger scales, like the ones relevant for particle physics experiments. This stemmed from the concept of effective field theories, which focus on specific energy scales and assume higher energy phenomena don't significantly impact them. But here's where things get interesting. String theory reveals that short-distance (ultraviolet) and long-distance (infrared) physics are deeply intertwined, challenging the notion of their complete decoupling.. In simpler terms, the microscopic world and the large-scale universe are not entirely separate, and what happens at one scale can influence the other.
This revelation challenges the notion that gravity can be completely ignored when exploring particle physics phenomena like the electroweak hierarchy problem. It suggests that a more comprehensive understanding might require incorporating the complexities of gravity, even at the energy scales currently probed by experiments.
Let me give you an example. Imagine colliding two gravitons, particles carrying the force of gravity, at extremely high energies. What would happen? Our intuition might suggest complete uncertainty, as such an experiment has never been conducted. But surprisingly, we can make educated guesses about the outcome. Why? Because when these gravitons approach each other at high energies, they get squeezed into an incredibly small region. This region becomes so dense that it essentially forms a microscopic black hole. Understanding the behavior of this black hole, however, falls under the realm of infrared physics, which deals with low-energy phenomena.
But one should note that this contradicts the traditional expectation in quantum field theories, where phenomena at different energy scales are often assumed to be independent. The implications extend beyond simple graviton scattering. String theory reveals that all quantum field theories emerging from gravity at low energies exhibit this remarkable intertwining of energy scales. This means that understanding particle interactions, typically described by these low-energy theories, might require considering the influence of high-energy phenomena through their connection to gravity.
In essence, gravity acts as a bridge, blurring the lines between the traditionally perceived separation of energy scales. This realization challenges our current understanding of particle physics and necessitates incorporating the complexities of gravity into the picture, even at energy scales accessible to current experiments.
Furthermore, string theory reveals surprising limitations on the types of quantum field theories that can emerge from low-energy descriptions of gravity. For instance, the number of possible supersymmetric theories is drastically reduced compared to the expectations of traditional quantum field theories. This constraint arises solely from the influence of gravity. Imagine choosing a random gauge group, like SU(N). In traditional theories, N could be any arbitrary number. However, string theory suggests a maximum rank of 22 for gauge group in N=4 supersymmetric theories, significantly limiting the possibilities.
This intertwining of quantum field theory and gravity has profound implications. It suggests that seemingly unrelated questions, such as the hierarchy problem, dark energy density, and neutrino mass, might find their answers through a deeper understanding of how gravity interacts with other forces at various energy scales. In essence, incorporating quantum gravity into the picture changes the "prior probabilities" of what is possible. Phenomena that seem unnatural in traditional frameworks might become more plausible when considering the constraints imposed by gravity. This necessitates a paradigm shift in our approach to particle physics, demanding a more unified understanding that integrates the complexities of gravity across all energy scales.
Can you explain us and give more examples on the role that string theory plays in understanding of the Universe?
Cumrun Vafa: String theory proposes a radical idea for unifying the fundamental forces, suggesting a universe with a maximum of 11 spacetime dimensions. This number isn't arbitrary; it's a constraint dictated by the theory. Despite our perception of only three spatial dimensions and one-time dimension, string theory implies that this configuration may have deeper significance.
Why not 10 billion dimensions? Why do gauge groups, representing forces, appear relatively small? These are the precise questions string theory seeks to address through heuristic connections. One such connection involves gravity. Traditionally, gravity is the weakest force compared to, for example, electromagnetism. String theory, in conjunction with black hole physics, introduces the weak gravity conjecture. This conjecture posits that gravity will always be the weakest force, regardless of the specific universe description.
Consider, for instance, a scenario where the electromagnetic force between two electrons weakens to the point where their gravitational attraction overpowers it. String theory, supported by observations, suggests this scenario is impossible within a quantum gravity system. Despite not violating traditional quantum theory, the presence of gravity imposes a specific hierarchy of forces. The weak gravity conjecture is just one example. String theory also implies constraints on spacetime dimensions and the complexity of gauge groups. Collectively, these observations suggest a deeper role for quantum gravity in shaping our universe.
While these connections rely on heuristic arguments, they provide intriguing insights into the fundamental principles governing our reality. Further exploration within string theory, alongside advancements in experimental observations, holds promise for unravelling the mysteries behind the apparently arbitrary features of our universe.
In summary, particle physics has made tremendous strides in recent decades, yet certain puzzles, such as the hierarchy problem, continue to elude satisfactory resolution. These challenges not only highlight the limitations of our current theoretical frameworks but also offer tantalizing clues about the underlying nature of reality. The interplay between quantum gravity and particle physics has emerged as a fertile ground for exploration, revealing unexpected connections and insights. As we unravel the mysteries of the universe, each new discovery brings us closer to a more comprehensive understanding of the fundamental forces at play and the fundamental nature of reality itself.
Your contributions to the understanding of the mathematical structures underlying string theory have been groundbreaking. What is the influence of mathematical concepts such as algebraic geometry and topology in your research and the development of string theory?
Cumrun Vafa: These branches of mathematics are crucial to string theory for several reasons. Firstly, string theory naturally exists in more than four dimensions. To connect it to our four-dimensional observations, we need a process called compactification. This involves choosing a compact, extra space – typically described using algebraic geometry – that “rolls up” the additional dimensions. The size and shape of this extra space, studied through topology, significantly impact the physics we observe in four dimensions.
Why is this important? One reason is that the spectrum of particles, the forces between them, and even the couplings (strengths of interactions) can all depend on the geometric and topological properties of this compactified space. What's the coupling between the Higgs boson particle and the electrons, for example, might depend on properties of geometrical properties of this manifold. Similarly, it can play a role in the couplings with other particles. This was so crucial for understanding our 4-dimensional physics. In essence, how these extra dimensions are "curled up" determines the nature of the four-dimensional world we experience.
Recently, there has been increasing interest in the concept of "swampland" criteria as a means of distinguishing between consistent quantum field theories and those that are inconsistent and not embeddable into a complete theory of quantum gravity. Could you explain what the swampland criteria entail and how they evolved over the years? Do other areas of physics affect this work?
Cumrun Vafa: I previously mentioned the swampland criteria, but let's delve deeper. Consider gravity as the weakest force and the existence of an upper bound on the gauge group rank in 4D supersymmetric systems. Initially, string theory's finite possibilities in the 4D realm compared to the infinite possibilities allowed by quantum field theory seemed peculiar. However, further exploration revealed this as a characteristic not unique to string theory, but potentially inherent to any conceivable quantum gravity theory.
Essentially, quantum gravity restricts the system to a finite set of possibilities, leaving an infinite number of otherwise viable quantum systems incompatible with its inclusion. These incompatible systems are categorized as belonging to the "swampland," contrasting with the "landscape" of viable theories.
Imagine a vast desert of potential theories, with a finite number of precious jewels scattered within. Finding these jewels directly would be incredibly challenging. However, the swampland program focuses on identifying characteristics that exclude theories, effectively eliminating vast swathes of the desert.
Instead of pinpointing the specific jewels (viable theories), it's easier to identify areas devoid of them (incompatible theories). This approach involves establishing criteria that disqualify theories, relegating them to the swampland. For example, a theory with gravity stronger than the strong nuclear force would be deemed incompatible.
By accumulating such exclusionary criteria, the swampland program progressively narrows down the potential locations of the jewels (viable theories). This ongoing effort has yielded numerous conditions pointing towards a surprisingly simple picture of quantum gravity.
While we haven't discovered a single, overarching principle encompassing everything, the identified principles exhibit remarkable consistency and reinforce each other. Our current understanding resembles the early days of quantum mechanics, where individual pieces like wave-particle duality and quantized angular momentum were gradually discovered. Similarly, the swampland program draws upon insights from string theory to establish these "rules of thumb" without possessing a definitive equation akin to Schrödinger's equation. This ongoing process has yielded valuable insights and even led to intriguing predictions about our universe.
Your recent paper, "Swamplandish Unification of the Dark Sector" explores how swampland ideas can be applied to understand dark matter and dark energy. Can you elaborate on this concept?
Cumrun Vafa: Our work builds on the idea of duality in string theory, which states that under certain conditions, different physical descriptions can represent the same underlying theory. When we take a physical theory to extreme values, its usual description breaks down, revealing a "tower of light particles" with exponentially decreasing masses that essentially form the fundamental ingredients of the theory. These light particles represent alternative descriptions of the theory.
Essentially, we quantified this by observing that as one approaches the boundary of these states, the tower of particles exponentially decreases in mass. It's important to note that it's not just a single particle experiencing this mass reduction; rather, it's an entire tower of particles, characterized by long wavelength gravity excitations in large emerging new dimensions or low energy vibrating modes of strings.
This principle, known as the "swampland conjecture," asserts that such a tower of light particles should consistently emerge in quantum gravity, unlike in quantum field theory, where examples exist wherein parameters may vary without such consequences. Thus, this feature seems to be unique to quantum gravity. This concept is encapsulated in what we refer to as the "distance conjecture," implying that extreme shifts in parameter space lead to the emergence of this tower of light particles, effectively illustrating a connection between distance and duality. The distance conjecture in swampland, suggests that such towers of light particles should always appear in theories with quantum gravity, unlike pure quantum field theories.
More recently, in collaboration with colleagues Dieter Lüst and Eran Palti, we observed that this idea extends beyond just coupling constants to encompass parameters like dark energy. Furthermore, in a recent paper authored with Miguel Montero, and Irene Valenzuela, we applied this notion to our understanding of the universe.
We recently extended this idea to other parameters, including the dark energy density of our universe (10-122 in fundamental units). The incredibly small value of dark energy suggests the existence of a corresponding tower of light particles. These particles are expected to be weakly interacting and have masses related to a power of the dark energy density.
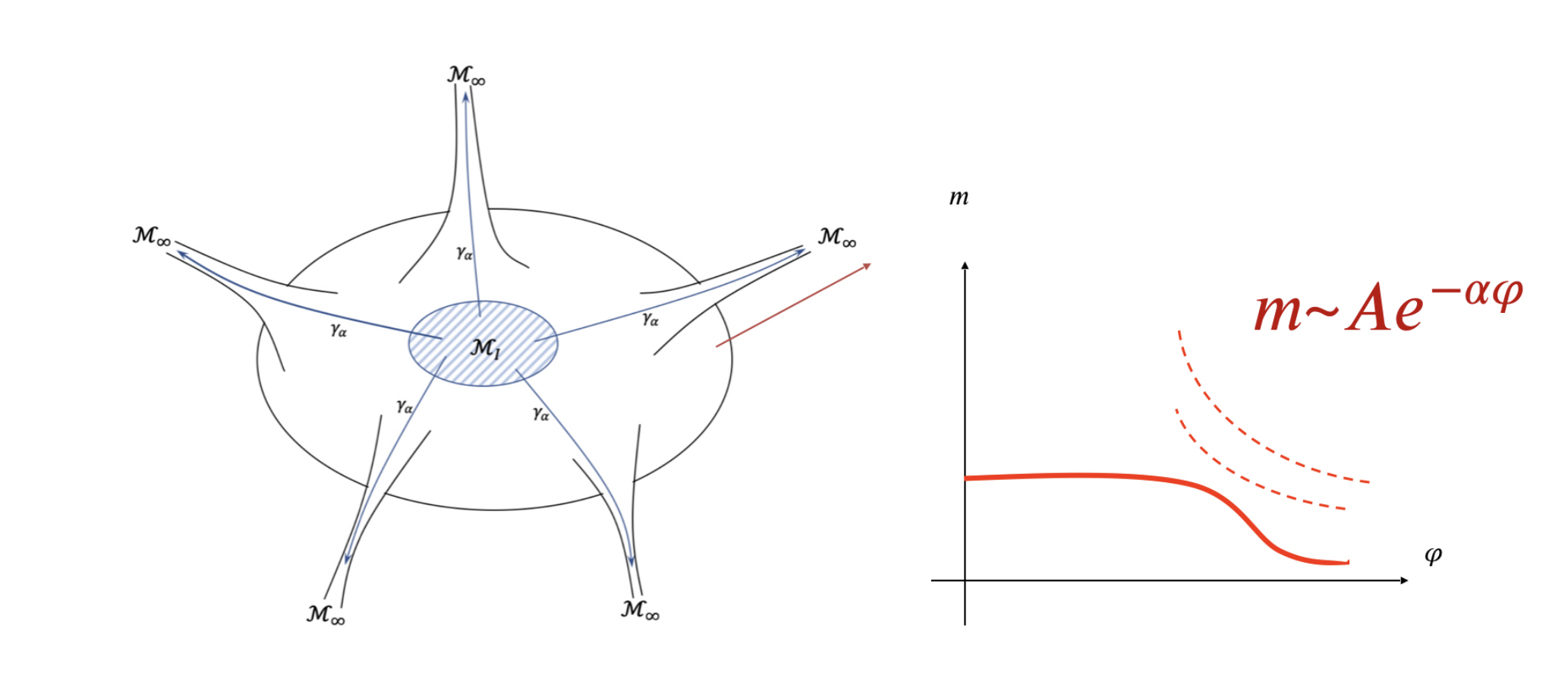
Figure 1: As we go to extreme values of field space, a tower of light particles emerge whose mass scales exponentially with field space distance. Source: https://arxiv.org/pdf/2402.00981.pdf
Interestingly, we propose that these very particles could be the dark matter we've been searching for. This approach suggests a fascinating link between dark matter and dark energy. The incredibly small amount of dark energy appears to be connected to the existence of a group of very lightweight particles. These particles, surprisingly, are thought to be the dark matter we've been searching for.
Naturally, this raises questions about these particles. Where do they come from? How do they interact with our world? Our research suggests that the most likely explanation, considering everything else we know about the universe, involves the existence of one extra mesoscopic dimension. This unique extra dimension helps explain the complex interplay between dark matter, dark energy, and the fundamental structure of the universe.
Furthermore, our theory suggests a novel consequence: the force law between particles should deviate from the usual Newton's inverse-square law at micron distances. This theory offers testable predictions with significant implications and experimentalists are currently working to test this. When two particles are brought within a micron of each other, Newton's familiar inverse-square force law is predicted to weaken, transitioning to a stronger force law described by one over r cubed. This shift towards a stronger force at shorter distances reflects the influence of an extra dimension. While current observations confirm the inverse-square law up to 30 microns, ongoing experiments are searching for this predicted deviation at the micron scale, providing a crucial test of the theory's validity.
What kind of experiments are involved in testing this theory?
Cumrun Vafa: These experiments fall under the category of precision force measurements. They typically involve a rotating attractor that attracts a torsion pendulum. By measuring the force between them, scientists can test for deviations from the expected force law.
However, achieving the necessary precision at these short distances is extremely challenging. Experiments need to carefully shield against electrical and other environmental noise that can interfere with the measurements. It's a very demanding task.
Are there any potential avenues for future experiments at colliders or observations that could provide evidence for or against this theory?
Cumrun Vafa: There remains much to be learned from forthcoming large-scale experiments, whether conducted in colliders, through astronomical observations, or via the detection of gravitational waves.
Regarding gravitational waves, however, insights specific to this particular theory may prove elusive. This is because the frequencies of gravitational waves generated by astrophysical phenomena are typically much lower than those required to excite modes in the extra dimension.
Nevertheless, alternative signatures may manifest, particularly in astrophysical phenomena such as structure formation. The decaying nature of the proposed dark matter particles could impact galaxy formation. The gradual decay of the dark matter tower into lighter components redistributes mass and imparts a kick velocity upon decay. This could manifest as subtle deviations in the observed structure of galaxies, particularly in their formation and evolution. Such deviations from predicted outcomes, if observed, could provide evidence supporting or refuting the proposed model.
Additionally, the Cosmic Microwave Background (CMB) offers another avenue for potential signatures. The decay of dark matter into photons could impact the CMB, as well as contribute to the extra-galactic background radiation. While these signals might be faint, advancements in observational techniques and data analysis could improve our ability to detect them in the future.
Interestingly, the theory's predictions regarding dark matter distribution align with certain observed tensions in cosmology, such as the s8 tension. This tension arises from discrepancies between predictions of the structures at a certain distance scale from the standard model of cosmology and observations in the universe. The reduced structure formation predicted by this theory could potentially explain these discrepancies, making it an intriguing candidate for further investigation.
And what about the role of the Higgs boson? Could the Higgs have played a role in the early universe?
In our exploration, we've observed a significant relationship between the electroweak hierarchy and the framework I've been discussing. This is an area of keen interest at CERN and elsewhere. Specifically, we've found that incorporating neutrinos into this scenario naturally involves the inclusion of right-handed neutrinos propagating within these higher dimensions. This notion of higher dimensions facilitating the description of right-handed neutrinos has been proposed by physicists for over two decades. What's intriguing is that the parameter ranges we're working with, involving micron-scale extra dimensions and right-handed neutrinos, perfectly align to yield the appropriate neutrino mass.
Furthermore, this framework not only accounts for the three active neutrinos but also predicts the existence of a tower of light neutrinos known as sterile neutrinos, which exhibit weaker coupling to our known particles. These sterile neutrinos could potentially manifest in various experiments, perhaps through observations related to short baseline anomalies or neutrino oscillations. A crucial aspect to consider is the mass comparison between these sterile neutrinos and the regular active neutrinos. While they could have inherently different masses, our framework suggests a scenario where the active and sterile neutrinos possess comparable masses, thereby hinting at a lack of hierarchy in the neutrino sector. This lack of hierarchy in the neutrino sector could be linked to the observed weakness of the electroweak force.
If I understand correctly, you are suggesting a connection between the weakness of this force and the mysterious dark energy?
Cumrun Vafe: Indeed. In the framework that we developed, it turns out that the scale of the electroweak force is actually tied to the scale of dark energy, albeit at a very large factor. This, in turn, suggests a deeper connection. Consequently, all fundamental parameters, including the Higgs mass, the Planck mass, and the mass of dark matter, become interconnected through the scale of dark energy, denoted by lambda.
This concept echoes the visionary idea proposed by Dirac, proposing a fundamental explanation for the vast disparities in physics scales. Remarkably, our findings propose that all these hierarchies can potentially be unified under one cosmic hierarchy—the minuteness of dark energy. In essence, this framework suggests a paradigm shift where the cosmological hierarchy, characterized by the infinitesimal magnitude of dark energy, serves as the unifying thread weaving together the intricate tapestry of physical hierarchies. We hope that it will inspire experimental physicists, paving new exciting avenues for exploration in particle physics and cosmology, potentially leading to a deeper understanding of the fundamental nature of our universe.
One key aspect worth exploring further is how to foster stronger collaboration between experimentalists and theorists.
An example that comes to mind is a project in Vienna which relates to measuring deviation from Newton’s inverse square law at the micron scale predicted from our theories. It underscores the importance of aligning experimental endeavours with theoretical expectations, thus enabling experimentalists to target specific regions of parameter space effectively. This synergy between theory and experiment is undeniably beneficial.
Institutions like CERN serve as exemplary models in this regard. With both experimentalists and theorists working hand in hand, ideas in particle physics are advanced collaboratively. This symbiotic relationship has proven fruitful, with experimentalists gaining insights from theorists and vice versa.
However, while this connection between experimentalists and theorists is generally robust, there's room for improvement in bridging the gap between phenomenological theorists and those focused on quantum gravity, such as practitioners of string theory. Currently, many traditional particle physicists, particularly those involved in phenomenology, may not be fully aware of the implications of quantum gravity theories. Consequently, they may overlook the relevance of gravity in their work. Recognizing gravity's significance is crucial, as it can profoundly influence quantum field theories and particle phenomenology. Ignoring this aspect poses a substantial oversight.
Therefore, enhancing collaboration and communication between these diverse branches of theoretical physics is imperative. Acknowledging the interplay between quantum gravity and traditional particle physics can lead to richer insights and more comprehensive frameworks for understanding the universe.
Could you offer some advice for young students who are considering to enter the field of theoretical physics today?
C. Vafa: Well, for those just stepping into theoretical physics, it might seem like a fractured landscape, with researchers delving into various areas. This diversity can be overwhelming, leaving one uncertain about where to focus or which path will lead to meaningful discoveries. My advice would be: don't give up. Follow your intuition and explore diverse avenues of study. While it may initially appear confusing, every direction contributes to our collective pursuit of truth. Young minds like yours are essential in pushing the boundaries of knowledge further. Despite the challenges of grappling with a vast array of concepts and activities, I encourage you not to be deterred by easier paths unrelated to physics. Stay curious and persevere in your pursuit of understanding.
Note: Professor Cumrun Vafa will deliver the CERN Colloquium on May 30th "Quantum Gravity and Predictions for our Universe". Find out more information about the event: https://indico.cern.ch/event/1393384/
