Introduction

The discovery of the electron in 1897 by Thomson, Wiechert and Kaufmann might be considered the starting date of elementary particle physics, as still today the electron is considered to be a fundamental particle. From there on it took another 36 years before Carl D. Anderson found its anti-particle, the positron, but only three more years passed and he found the muon (together with Seth Neddermeyer) in 1936. At first sight, the muon and the electron looked very different, the first one being nearly mass-less and stable, while the latter one being a factor 200 heavier and decaying with a half-life-time of ≈2.2x10^-6 seconds. Another 39 years later, the tau lepton was found in 1975 and Martin L. Perl received the Nobel Prize for this discovery in 1995. This lepton looked even more different than (despite having the same charge) the electron and the muon as it is quite heavy (≈1.78 GeV), has a very short life-time of 3x10^-13 second and can decay into many different final states.   

However, within the advent of the Standard Model (SM) of particle physics in the late 1960s, it was recognized that the electron, muon and tau leptons have after all very similar properties. They all interact with the photon and the weak gauge bosons (W and Z) in exactly the same way. In fact, only the interactions with the Higgs boson, parametrized by the so-called Yukawa couplings, distinguish an electron from a muon and from a tau lepton. While these couplings give rise to the lepton masses, leading to the huge differences in lifetime, they are in fact tiny; ranging from 10^-4 for the electron to 1% for the muon, which is small compared to the gauge couplings of around 0.5. Therefore, the SM interactions are to a very good approximation the same for all three leptons and are therefore said that the SM (approximately) respects lepton flavour universality (LFU), despite the seemingly large differences in lifetimes originate from phase space effects. 

The SM has been extensively tested and confirmed within the previous half a century, with the discovery of the Higgs boson in 2012 by the LHC being the last missing piece. Nonetheless, it is widely accepted that the SM cannot be the ultimate fundamental theory of physics, as, e.g., it cannot account for neutrino masses, for the dominance of matter over anti-matter in our Universe, and it does not include gravity nor a candidate for dark matter. Therefore, many extensions of the SM have been proposed within the last decades, which predicted new particles within the reach of high-energy colliders. However, the hopes for direct discoveries of new particles (first at the Tevatron, then at the LHC), such as supersymmetric partners of the SM particles or composite and extra-dimensional excitations of SM particles, were not fulfilled so far. This also challenged the believe that the ultimate theory of physics could be found in a top-down approach and shifted the focus towards a bottom-up approach based on experimental results showing deviations from the SM. As the high-energy collider searches yielded null results for new resonances, the indirect search for physics beyond the SM (BSM) via precision experiments has become an increasingly important avenue. 

Among the indirect searches, flavour observables (i.e., processes looking for rare transitions among the different generations of quarks and leptons), and in particular observables measuring LFU violation (LFUV), are especially promising since they are stringently suppressed in SM and thus very sensitive to new physics (NP). In fact, in recent years a coherent pattern of anomalies all pointing towards LFUV emerged. A tension in the anomalous magnetic moment of the muon (g-2)_μ, an effect originating only from quantum fluctuations (called loop-level), has prevailed since 2006 and has very recently been confirmed by the muon g-2 experiment at Fermilab. Furthermore, since 2014 the LHCb experiment at CERN, supported by measurements of the Belle experiment at KEK, accumulated signs for BSM physics in decays of B mesons (quark bound-states involving a heavy bottom quark) involving leptons in the final state. Again, this has recently been confirmed by the measurement of the ratio R(K), in which LHCb reported for the first time evidence for LFUV new physics. Interestingly, all these observations show that electrons and muons behave unexpectedly differently, such that a correlation between the B meson decays and (g-2)_μ seems plausible. Finally, a tension in nuclear beta decays (a form of radioactive decay) was observed, which, as recently shown, can as well be interpreted as a sign that electrons and muons are more different than predicted by the SM, and also the CMS experiment at CERN observed more very high energetic electrons than expected. Altogether, this poses the question if lepton, in particular muons and electrons are more different than expected within the SM after all. 

Hints for Lepton Flavour Universality Violation

As outlined in the introduction, intriguing hints for the violation of LFU have been accumulated within recent years which challenge the SM. They can be divided into five different classes of observables which all disagree from the SM predictions, as shown in Fig. 1. Let us now have a more detailed look at these “anomalies”.

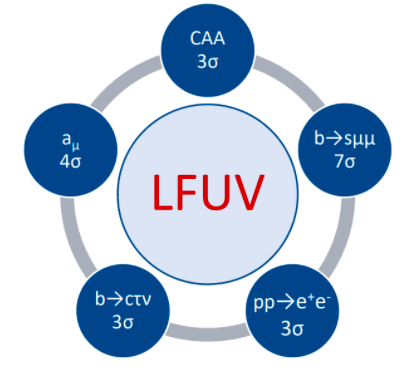
Figure 1: Compilation of the hints for lepton flavour universality violation (LFUV) together with their significance in terms of standard deviations.

The b→sℓ⁺ℓ^-  class of interactions

The abbreviation b→sℓ⁺ℓ^- stands for a whole class of processes which involve, at the fundamental quark level, the transition of a heavy bottom quark (b) to a strange quarks (s) and pair of oppositely charged leptons (ℓ), which could either be an electron (e) or a muon (μ). As the bottom and strange quark have the same electric charge, such a transition is called a “flavour changing neutral current” (FCNC) process. As all FCNCs, b→sℓ⁺ℓ^- transitions are strongly suppressed in the SM: They only arise via quantum fluctuations (called loop effects) since the sole source of flavour violation in the SM is the Cabbibo-Kobayashi-Maskawa (CKM) matrix, entering the coupling of the charged W boson to quark. Furthermore, it is suppressed by the weak scale and by the smallness of off-diagonal elements of the CKM matrix (see Fig. 2). 

Figure 2: From left to right: Feynman diagram showing the W coupling to quarks, involving the CKM matrix V. Notation for the up and down-type quarks as vectors in flavour space. CKM matrix with the size of the coloured squares showing the absolute values of the elements. Therefore, this class of processes is very sensitive to NP. 

Among the b→sℓ⁺ℓ^- processes, the ratios: R(K) = B --> Kμ⁺μ^- / B --> Ke⁺e^- and R (K*) = B--> K*μ⁺μ^-/ Β --> Κ*e⁺e^- measured most precisely by LHCb [1], are particularly prominent and interesting.

In principle, for the prediction of these “semi-leptonic decays” (they are named this way since they involve leptons as well as a meson in the final state) quantities called “form factors” (governing the probability of a B meson decaying into a kaon, or excited kaon (K*)) are needed, which have to be calculated with non-perturbative QCD methods.

These methods have intrinsic uncertainties and therefore the from-factors are only known with an accuracy of 10-20%. Nonetheless, the SM predictions for both ratios are every clean. The reason for this is that the muon mass as well as the electron mass can be neglected (compared to the B mass) and thus one expects to measure in principle unity in the SM, as in in setup with lepton flavour universality conservation. Intriguingly, LHCb found values significantly below one and even reported recently first evidence for LFUV in R(K) (see Fig. 3). 

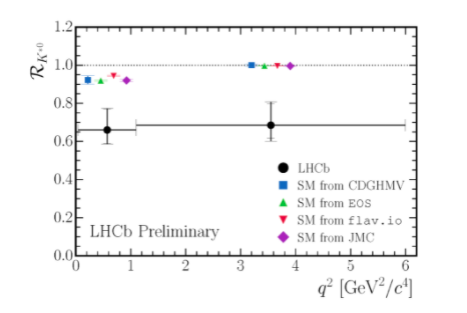
Figure 3: Experimental values of the ratios R(K) (top) and R(K*) (bottom). On can see that in both cases the observed values are smaller than the SM expectations.

Furthermore, these hints for LFUV new physics are e.g. supported by the measurements of the angular observable called P5’ in B --> K* μ⁺μ^- and the decay Β_s --> φμ⁺μ^- , which were also measured already some time ago by LHCb and confirmed recently (see Fig. 4). Importantly, these anomalies are consistent with all other available measurements of b→sℓ⁺ℓ^- transitions. Therefore, global fits find a preference for NP compared to the SM hypothesis of up to 7σ and even slightly more once the latest LHCb updates are included [2].

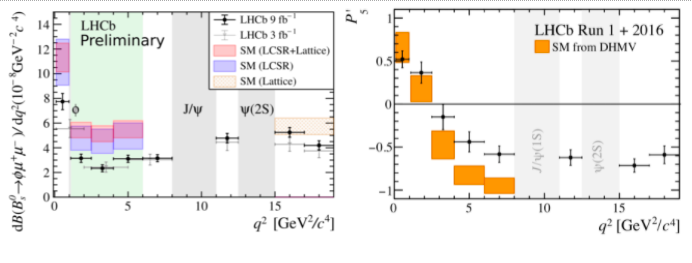
Figure 4: The total branching ratio for Β_s --> φμ⁺μ^- (left) and the angular observable P5’ (right) as measured by LHCb. Again, one can see that the data supports destructively interfering NP effects w.r.t the SM.

The anomalous magnetic moment (g-2)_μ

The anomalous magnetic moment of charged fermions was a key prediction of the Dirac equation (where it equals exactly 2) and was later used to confirm quantum electro dynamics where the measurement agreed with the deviation from 2 predicted by Schwinger (corresponding to diagram a) in Fig. 5). Ever since, it served as a precision test of the SM and first indications for beyond the SM effects were found in 2006 by the E821 experiment at Brookhaven [3]. This measurement was recently confirmed by the g-2 experiment at Fermilab [4] and the combined result displays a 4.2σ tension with the SM prediction of the “g-2 Theory Initiative” [5]. The main theory uncertainty comes from a contribution called “hadronic vacuum polarization” (HVP), corresponding to diagram d). Here, the Budapest Marseilles Wuppertal (BMW) lattice collaboration released first results that indicate a value in tension with the one derived from e⁺e^- data [6], however, future detailed comparisons with other lattice calculations will be necessary to achieve the same level of scrutiny that has become standard for the data-driven approach.

As any deviation from 2 in the anomalous magnetic moment of this muon is only generated at the loop level, the overall size of the NP contribution required to reconcile theory of the SM prediction is not small. In fact, it is of the same order as the leading electroweak contribution of the SM induced by W and Z exchange (diagram b) and c)). 

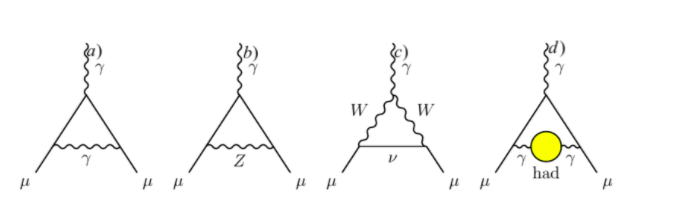
Figure 5: Feynman diagrams contribution to the anomalous magnetic moment of the muon within the SM.

The b→cτν channel

Unlike the FCNC processes b→sℓ⁺ℓ^-, b→cτν is a charged current and is thus already mediated at tree-level in the SM and the corresponding decays have much higher probabilities to occur and therefore also bigger branching ratios.  The most prominent examples of observables involving b→cτν at the fundamental level, are the ratios

and .

Here, the mass of the tau lepton cannot be neglected compared to the B meson mass and therefore the SM prediction is much smaller than one (as the tau mode is suppressed by phase space). Furthermore, the non-negligible tau mass leads to an imperfect cancellations of the form factors in the ratio and thus the resulting SM prediction (see black cross in the Fig. 6) is not as precise than the ones for R(K) and R(K*).

Nonetheless, the measurements of Belle, BaBar and LHCb are consistently above the SM prediction resulting in a combined tension of 3 sigma according to the Heavy Flavour Averaging Group (HFLAV) [7]. Importantly, as these processes are mediated at tree-level a significant NP effect would be required to account for the corresponding anomaly.

Figure 6: Compilation of the measurements of R(D) and R(D*) and the comparison to the SM predictions performed by HFLAV.

CAA 

This abbreviation stands for “Cabbibo Angle Anomaly” where the Cabbibo angle parametrizes the mixing among the first two generations of quarks, i.e. the top-left 2 by 2 sub-block of the CKM matrix (see Fig. 2). As the CKM matrix is unitary, it must fulfil the requirement that the sum of the squares of the elements in one row or in one column must add up to unity. This unitarity relation can be used to check the consistency of different determinations of CKM elements within the SM and thus also to search for NP.

Interestingly, a deficit in the first row unitarity at the 3σ level is observed [8]. This can be traced back to the fact the V_ud extracted from super-allowed beta decays (a specific class of radioactive nuclear beta decays) does not agree with V_us determined from kaon and tau decays. Interestingly, this deviation can also be interpreted as a sign of LFUV [9] since beta decays involve electrons while the most precise determination of V_us comes from decays with final state muons. Here, the SM contribution is at tree-level, but a relative NP effect at the sub per mille level suffices to explain it.

pp→e⁺e^- 

In the search for high-energetic lepton pairs the CMS experiment found more electrons than expected while the number of observed mouns agreed with the SM prediction [10]. The significance of the excess is around 4σ, is compatible with the analogous ATLAS analysis [11], however when accounting for it via NP, only 3σ out of the 4σ can be explained. As the electrons are “non-resonant”, meaning that they do not originate from a new directly produced particle, a NP explanation must involve heavy particles above the LHC energy scale. 

Explaining the hints for LFUV beyond the SM

Since the LFUV anomalies form such a coherent pattern (see Fig. 1), it is only natural to ask how they could be explained in terms of extensions of the SM by new particles and new interactions. First of all, in order for such an extension to be consistent (renormalizable), one can only add a few new types of particle: scalars (spin 0), fermions (spin 1/2) and vectors (spin 1). For the latter possibility, a consistent extension requires some spontaneous symmetry breaking via a Higgs mechanism or some composite or extra-dimensional dynamics. In particular, we will consider leptoquarks (LQs) as possible solutions of the flavour anomalies. These are new particles which couple a quark directly to a lepton, unlike any interaction in the SM. Such particles were predicted in the context of Grand Unified Theories which unite the SM gauge interactions by postulating a bigger symmetry group, such that they are vector particles. Alternatively, they can also be scalar particles, similar to the Higgs. There are different kinds (also called representations) of LQs which differ by their interactions to SM gauge bosons. Some of them can lead to proton decays, and are therefore stringently constrained by the non-observation of it while other representations are free of proton decay.

The b→sℓ⁺ℓ^- channel

Here three different classes of solutions are possible:

• A neutral Z’ boson (a heavy version of the SM Z) with a flavour violating couplings to bottom and strange quarks can account for the anomaly at tree-level [12]. Even though one in general expects an effect in B_s mixing, and it can be produced resonantly at the LHC, such a solution is still possible. In fact, in order to fully cover the expected allowed parameter space for a Z’, the FCC-hh would be necessary.
• LQ representations can already contribute at tree-level to b→sℓ⁺ℓ^- while giving loop-suppressed effects in other observables [13]. Therefore, they can account for the anomaly without being in tension with other observables. 

Furthermore, one could also explain b→sℓ⁺ℓ^- via a loop-level involving new heavy scalars and fermions [14].

The b→cτν process

As this process is mediated at tree-level in the SM, also a tree-level NP contribution is necessary to obtain the desired effect which needs to be of the order of 10% w.r.t the SM. As it is a charged current process, the only possibilities are a charged Higgses (a singly charged scalar, neutral under QCD), W’ bosons (a heavy version of the SM W) and LQs. The first two options are disfavoured by the B_c lifetime and/or LHC searches, leaving LQ as the best option for a full explanation [15]. However, also in this case, a solution is not trivial, as constraints from B_s mixing, B->K*νν and LHC searches must be avoided. 

Measuring the CAA

To determine V_ud from beta decays the Fermi constant (which parametrizes the effective interaction strength of the weak force at low energies), measured in muon decay, is needed. However, the value of the Fermi constant can be different from the one of the SM in the presence of NP. Taking this into account the CAA can be explained via a [16]:

1. direct (tree-level) modification of beta decays
2. direct (tree-level) modification of muon decay
3. modified W-μ-ν coupling
4. modified W-u-d couplings. 

Option 1) could be realized by a W’ or a LQ, however in the latter case stringent bounds from other flavour observables arise. Possibility 2) could be achieved by adding a new leptophilic scalar or vector boson to the SM while option 3) and 4) can be realized by heavy new leptons and quarks, respectively, but also by W-W’ mixing. 

pp→e⁺e^-

Here explanation can be provided by NP coupling to first generation quarks and electrons with O(1) couplings and masses around 10 TeV that interferes constructively with the SM [17]. Therefore, a Z’ boson or a LQ coupling to electrons and first generation quarks have the potential to explain this CMS measurement.

Conclusions and Outlook

From the considerations above, we can see that the different anomalies point towards different extensions of the SM. These implications for new particles are summarized in Fig. 7 where the thickness of the error represents my very personal view on how strongly the different measurements point towards different new particle. One can see that an extension by a single new field cannot explain all anomalies. On the one hand, this could indicate that not all anomalies might be confirmed in the future. On the other hand, it is of course possible (and maybe even likely) that the SM is superseded by a more complicated theory with a sizable number of new degrees of freedom. In fact, there is also a slight tension in τ→μνν vs τ→eνν and μ→eνν which points towards LFUV and the Z→bb forward backward asymmetry measured by LEP could also point towards related NP [18]. Furthermore, the PEN experiment at PSI is expected to release soon new results on the ratio R(π)=π→μν/π→eν which is also an excellent probe of LFUV.

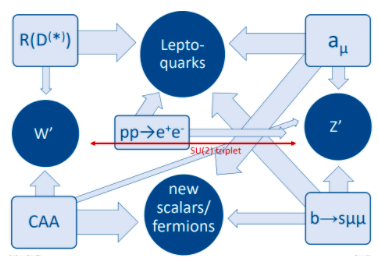
Figure 7: Anomalies and their implications for possible extensions of the SM be new particles. The thickness of the error indicates by very personal view, how strongly the hints for LFUV point towards a specific extension.

Importantly, even if only one of the anomalies will be confirmed, this would prove the existence of NP at the (multi) TeV scale, such that the new particles could not only be detected directly at the LHC or a future collider like the FCC, they would also have an impact on other precision observables, allowing for complementary determinations of their properties. As an example, we show the predictions for Higgs and Z decays to muons (h→μμ and Z→μμ) in the two different scalar LQ models which can explain g-2 of the muon in Fig. 8 [19,20]. Note that one representation predicts a constructive effect in h→μμ, while the other one predicts a destructive one, meaning that the two possibilities can be distinguished by future precision measurements. Even though the correlations for Z→μμ are less direct, a future Z factory, like the FCC-ee should be able to observe the predicted deviations from the SM expectations in this mode.

Finally, any extension of the SM accounting for the flavour anomalies could also be related to Dark Matter or neutrino masses, the observed matter anti-matter asymmetry and would have an impact on the evolution of our early universe. Furthermore, the discovery of a new particle, or even a whole NP sector, would be invaluable for any theoretic consideration regarding the ultimate fundamental theory of nature.

Figure 8: Upper plots: Predictions for h→μμ (w.r.t its SM value) as a function of a_μ=(g-2)_μ/2 for the two different LQ representations Φ₁ and Φ₂ that can account for the Brookhaven/Fermilab measurement. Lower plot: Predictions for the axial coupling of the Z boson to muon () for the same two LQ representations. Here the prediction depends on λ^t₂₃ and λ^R₂₃, the LQ couplings to muons and left- and right-handed top quarks, respectively. The green regions show the estimated sensitivity of future colliders. Note that FCC-ee possesses a clear discovery potential to observe such a modified Z coupling to muon.

References

1. LHCb Collaboration, R. Aaij et al., arXiv:2103.11769., LHCb Collaboration. R. Aaij et al., Test of lepton universality with B0 → K∗0 l`+l`− decays, JHEP 08 (2017) 055, [arXiv:1705.05802].
2. M. Alguero, B. Capdevila, S. Descotes-Genon, J. Matias, and M. Novoa-Brunet, in 55th Rencontres de Moriond on Electroweak Interactions and Unified Theories (2021) arXiv:2104.08921 [hep-ph]. W. Altmannshofer and P. Stangl, (2021), arXiv:2103.13370 [hep-ph].
3. T. Hurth, F. Mahmoudi, D. M. Santos, and S. Neshatpour, (2021), arXiv:2104.10058 [hep-ph]
4. G. W. Bennett et al. (Muon g-2 Collaboration), Final report of the Muon E821 anomalous magnetic moment measurement at BNL, Phys. Rev. D 73, 072003 (2006).
5. B. Abi et al. [Muon g−2 Collaboration], Phys. Rev. Lett. 126, no.14, 141801 (2021) doi:10.1103/PhysRevLett.126.141801 [arXiv:2104.03281 [hep-ex]].
6. T. Aoyama, N. Asmussen, M. Benayoun, J. Bijnens, T. Blum, M. Bruno, I. Caprini, C. M. Carloni Calame, M. Cè and G. Colangelo, et al., Phys. Rept. 887, 1-166 (2020) doi:10.1016/j.physrep.2020.07.006 [arXiv:2006.04822 [hep-ph]].
7. S. Borsanyi, Z. Fodor, J. N. Guenther, C. Hoelbling, S. D. Katz, L. Lellouch, T. Lippert, K. Miura, L. Parato and K. K. Szabo, et al., doi:10.1038/s41586-021-03418-1 [arXiv:2002.12347 [hep-lat]]
8. Y.Amhis C. Helsens, D. Hill, O. Sumensar. Prospects for B+c → τ+ντ at FCC-ee, arXiv:2105.13330v1 [hep-ex
   Particle Data Group Collaboration, P. A. Zyla et al., “Review of Particle Physics,” PTEP 2020 (2020) 083C01
9. A. Crivellin and M. Hoferichter, Phys. Rev. Lett. 125, 111801 (2020), 2002.07184
10. A. M. Sirunyan et al. (CMS) (2021), 2103.02708.
11. G. Aad et al. (ATLAS), JHEP 11, 005 (2020), 2006.12946.
12. W. Altmannshofer, P. Stangl, and D. M. Straub, Phys. Rev. D 96, 055008 (2017), 1704.05435
13. G. Hiller and M. Schmaltz, RK and future b→sℓℓ BSM opportunities, DOI:10.1103/PhysRevD.90.054014, arXiv:1408.1627 [hep-ph]
14. B. Gripaios, M. Nardecchia and S. A. Renner, JHEP 1606, 083 (2016) [arXiv:1509.05020 [hep-ph]].,P. Arnan, L.
15. Hofer, F. Mescia and A. Crivellin, JHEP 1704, 043 (2017) doi:10.1007/JHEP04(2017)043 [arXiv:1608.07832 [hep-ph]].
16. D. A. Faroughy, A. Greljo and J. F. Kamenik, Phys. Lett. B 764, 126 (2017) [arXiv:1609.07138 [hep-ph]].
    A. Crivellin, M. Hoferichter, and C. A. Manzari (2021), 2102.02825.
17. A. Crivellin (Zurich U. and PSI, Villigen), C. A. Manzari (Zurich U. and PSI, Villigen), M. Montull (Zurich U. and PSI, Villigen),
    e-Print: 2103.12003 [hep-ph].
18. A. Crivellin(CERN and PSI, Villigen and Zurich U.), C A Manzari(PSI, Villigen and Zurich U.), M. Alguero (Barcelona, Autonoma U. and Barcelona, IFAE), J. Matias (Barcelona, Autonoma U. and Barcelona, IFAE) (Oct 27, 2020). e-Print: 2010.14504 [hep-ph]
19.  A. Crivellin (CERN and Zurich U. and PSI, Villigen), D. Mueller(Zurich U. and PSI, Villigen), F. Saturnino (Bern U.) (Aug 6, 2020), e-Print: 2008.02643 [hep-ph]
20. A. Crivellin (CERN and Zurich U. and PSI, Villigen), C. Greub (U. Bern, AEC), D. Müller (Zurich U. and PSI, Villigen), F. Saturnino (U. Bern, AEC), e-Print: 2010.06593 [hep-ph]. DOI: 10.1007/JHEP02(2021)182./JHEP 02 (2021),182.