Even though the Standard Model of Particle Physics is incredibly successful and provides extremely accurate predictions for many physical quantities and mechanisms, the model is known to be incomplete. For instance, it fails in explaining the staggering abundance of matter compared to antimatter observed in our Universe. This inspires experiments to study the fundamental properties of matter/antimatter conjugates with ultra-high precision.

One of those is the Baryon Antibaryon Symmetry Experiment (BASE) at the AD/ELENA facility of CERN, which compares the fundamental properties of protons and antiprotons, providing extremely stringent tests of Charge, Parity & Time reversal (CPT)-invariance. One example is the measurement of the antiproton magnetic moment with 1.5 parts-per-billion fractional precision [1], which improved previous best measurements by a factor of more then 3000.  This article focuses on BASE’s latest measurement campaign [2], which was dedicated to measuring the proton-to-antiproton charge-to-mass (q/m) ratio R_{p, ̄p}. A value of: 

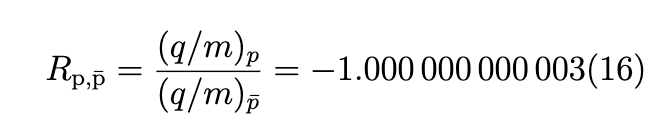
was derived, which has an unprecedented precision of 16 parts per trillion (p.p.t.). The campaign also provides a test of the Weak Equivalence Principle by comparing proton and antiproton clocks over the course of one and a half years.

Testing CPT-symmetry at the 16-parts-per-trillion level

The BASE setup consists of an advanced multi-Penning-trap system, where charged particles are trapped in a combination of an ultra-stable, axial 1.9 T magnetic field B₀ and an electrostatic quadrupole potential generated by a stack of cylindrical ring-shaped electrodes. In such a combination of static fields the trajectory of a trapped charged particle is a superposition of three independent harmonic motions: an axial motion along the magnetic field lines at frequency ν_z ≈640 kHz, a fast radial motion at modified cyclotron frequency ν₊ ≈ 29.65 MHz and a slow radial motion at magnetron frequency ν₋≈ 6.9 kHz. The cyclotron frequency ν_c of the trapped particle can be determined via the invariance theorem: 

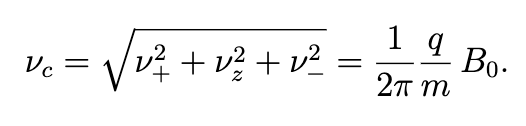
A schematic drawing of the BASE trap-stack is shown in Figure 1(a). A cloud of antiprotons and negatively charged hydrogen (H⁻) ions is stored in the reservoir trap on the left, from which single particles are extracted when required. The basic principle of the experiment is then to alternately shuttle an antiproton and an H⁻  ion into an ultra-stable and highly homogeneous measurement trap, as illustrated in Fig.1(b), where their respective cyclotron frequencies are determined. At the reported fractional precision, an H⁻ion is a perfect proxy for the proton [3], reducing systematic uncertainties imposed by trap polarity changes by orders of magnitude. The ratio of the two cyclotron frequencies cancels the magnetic field (to first order) and gives a direct measure of R_{p, ̄p.}

The power of BASE is that the three eigenmotions can be measured in a non-destructive way by ultra-sensitive tunable image-current detectors. When a single trapped antiproton or H⁻ ion oscillates along the trap axis, tiny image currents on the order of femto-ampere are induced in the cylindrical trap electrodes. By connecting a carefully tuned, ultra-sensitive superconducting RLC circuit to one of the trap electrodes, the axial oscillation frequency is imprinted onto the resonance curve of the circuit, as shown in green in Figure 1(d). The radial modes can be measured by inducing classical Rabi oscillations between the axial mode and the radial mode using the appropriate radiofrequency drive, resulting in the two sidebands shown in red in Figure 1(d), from which the radial frequency can be calculated. Alternatively, ν₊ can be measured directly by exciting the mode and picking up the image current with a dedicated detector, resulting in the peak spectrum shown in Figure 1(e). These techniques allow one charge-to-mass ratio comparison in about 240 s, about a factor of 50 times faster than in previous antiproton/proton comparisons [4].

Using both methods, about 24000 cyclotron frequency ratios were measured between December 2017 and May 2019, resulting in the reported 16 p.p.t. comparison. This improves the previous measurement [3] by a factor of 4 and tests the Standard Model with an energy resolution of approximately 2 ×10⁻²⁷ GeV, improving limits on 10 coefficients that constrain exotic interactions. 

Reaching this outstanding precision was made possible by considerable experiment stability improvements developed in recent years. These involved the redesign of the cryogenic setup, homogenization of the trap’s magnetic field, and the implementation of an advanced multi-layer magnetic shielding system. In addition, the dominant systematic uncertainty of the previous campaign was suppressed by developing an ultra-sensitive frequency-tunable detection system, which eliminates systematic shifts related to the interplay of trap-voltage tuning and residual magnetic field gradients.

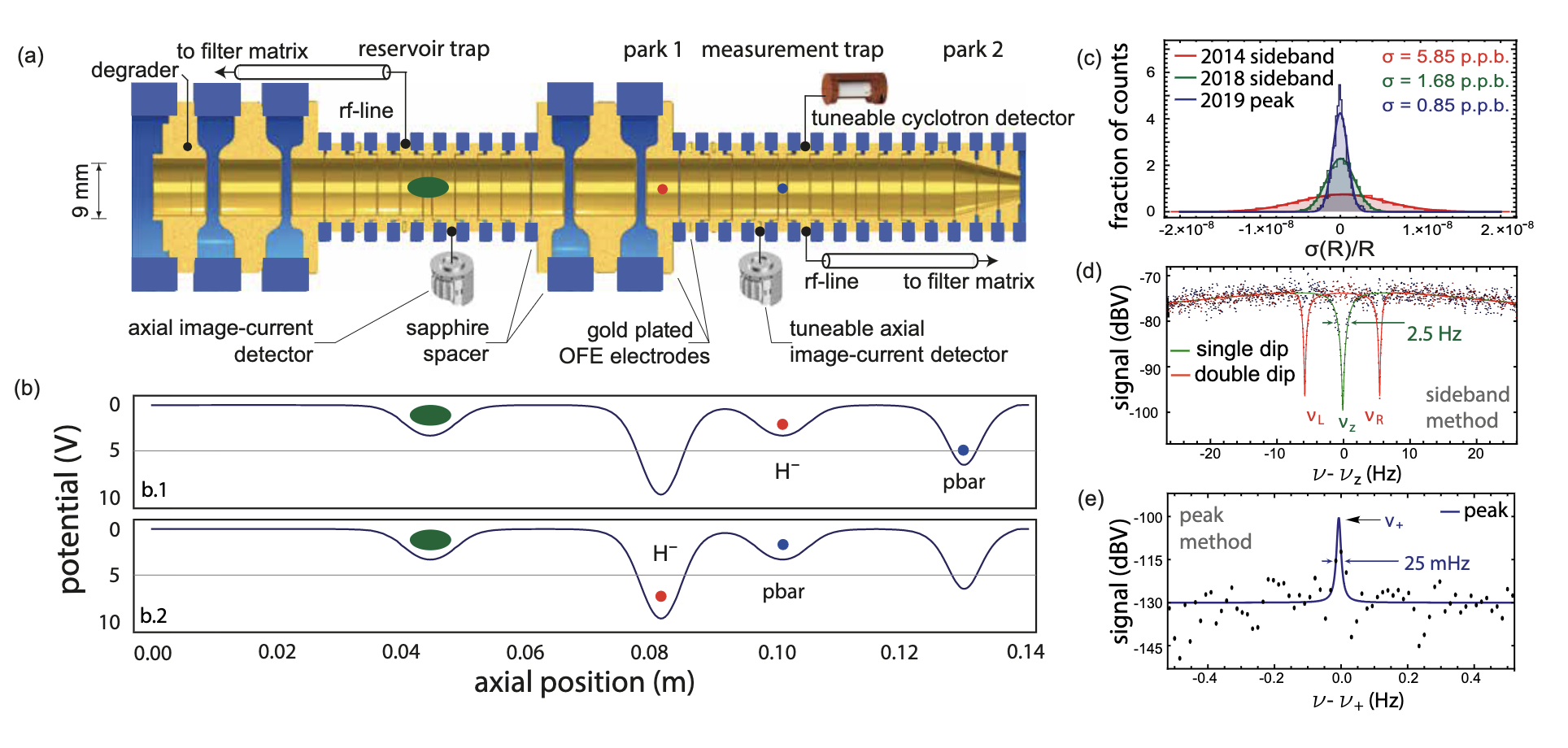
Figure 1: (a) Elements of the BASE experiment illustrating the setup, (b) the potentials for measuring the hydrogen ion and antiproton respectively, (c) the cyclotron frequency ratio fluctuations of the 2014 campaign and the latest campaign, (d) the signals on the axial detector and (e) the signal on the cyclotron detector.

First differential test of the Weak Equivalence Principle for antimatter clocks

One of the most desired experiments in antimatter physics is the direct test of the gravitational interaction of antimatter. Two types of measurements are distinguished - clock (WEPc) and free fall (WEPff) Weak Equivalence Principle tests. Currently, the similarity of these two different approaches is discussed controversially.

According to the interpretation of Hughes and Holzscheiter [5], if the coupling between matter and antimatter to gravity would be different, i.e. the Weak Equivalence Principle would be violated, a difference in measured cyclotron-clock-frequencies would be observed when measured at the same gravitational potential Φ_G. Using Φ_G of the local supergalactic cluster, BASE constrains the WEPc violating parameter to |α_g,_G −1|< 1.8 ×10⁻⁷, which improves the previous limit by a factor of 4.3. However, this interpretation was found controversial due to a potential lack of understanding of the gravitational potential.

To eliminate this unknown, we compare the cyclotron frequencies at different times throughout the year, effectively sampling the matter and antimatter clock frequencies at different gravitational potentials thanks to the elliptic trajectory of the Earth around the Sun. As shown in Figure 2, our measurements cover about 80% of the peak-to-peak variation of the gravitational potential, which allows us to constrain the WEPc violating parameter to |α_g,_D−1|< 0.030 (C.L.0.68) without making assumptions about the absolute gravitational potential. The presented result is at the anticipated precision level of experiments that plan to measure the free fall of antihydrogen and test the WEPff [6, 7, 8].

Figure 2: a) Variation of the gravitational potential in the BASE laboratory sourced by the elliptical orbit of the Earth around the Sun illustrated in b). The yellow points represent the data-taking windows.