An all-round boosted chase for supersymmetry

It is rare for a theory to inspire as much experimental attention as supersymmetry has. CMS completed more than 40 SUSY searches in Run 2 alone, reflecting how compelling this framework remains in the quest for new physics. SUSY proposes that every known particle has a heavier partner, a “superparticle”, and through its elegant theoretical structure offers solutions to several outstanding puzzles, from the hierarchy problem to the nature of dark matter. The theory, however, is highly flexible: it contains many free parameters and provides no unique prescription for how the superparticle spectrum should look. This freedom translates into an enormous range of possible masses and decay patterns, each leading to distinctive signatures in the detector. Each analysis helps to narrow this space, gradually updating the “SUSY configuration file” that nature has not supplied.
One common class of final states arises when a superparticle is much heavier than the particles into which it decays. In this case, a large fraction of the heavy particle’s mass is converted into the motion of the lighter particles, giving them a strong Lorentz boost. If these boosted particles themselves decay, their products are emitted close together, so that in the detector they appear to merge into a single, larger structure known as a boosted object. The larger the mass difference, the stronger the boost, making boosted objects a powerful handle for probing SUSY particles with very high masses.
Boosted-object final states arise in many SUSY scenarios, especially those motivated by naturalness, which predict gluinos and third-generation squarks with masses around the TeV scale. These sparticles can decay, either directly or through cascades involving other SUSY particles, to the stable lightest neutralino (which is the lightest SUSY particle in many models, and a well-known dark matter candidate) together with boosted W, Z, or Higgs bosons, or top quarks. The result is a striking final state containing boosted particles and a momentum imbalance in the transverse plane, that is, missing transverse momentum. In other cases, the SUSY particles themselves can appear as boosted objects. This occurs in scenarios with R-parity violation (RPV), where the lightest SUSY particle is unstable and decays entirely into standard model particles. Here, the boosted object is a high-momentum RPV particle, much heavier than its visible decay products.
Previous SUSY searches have focused on boosted objects, but typically addressed very specific final states. CMS recently released a new search, the razor boost analysis, which for the first time brings these signatures together in a systematically inclusive framework. The search probed a wide range of final states containing boosted W, Z, and Higgs bosons, as well as boosted top quarks. and to some extent, boosted SUSY particles. The boosted standard model particles decaying hadronically appear as large radius jets with mass and substructure, and were identified using machine learning techniques. The analysis employed the ParticleNet algorithm, a deep neural network trained to distinguish between boosted hadronic decays of heavy SM particles and jets originating from QCD multijet processes. For the first time in a SUSY search, the analysis also investigated final states with boosted leptonic jets -- boosted objects whose decays include a lepton. Such objects arise, for example, from leptonic decays of boosted top quarks, or RPV SUSY particles decaying into leptons. These signatures are captured by identifying nonisolated leptons in the vicinity of a large-radius jet. Figure 1 illustrates two representative SUSY processes that give rise to boosted-object signatures.
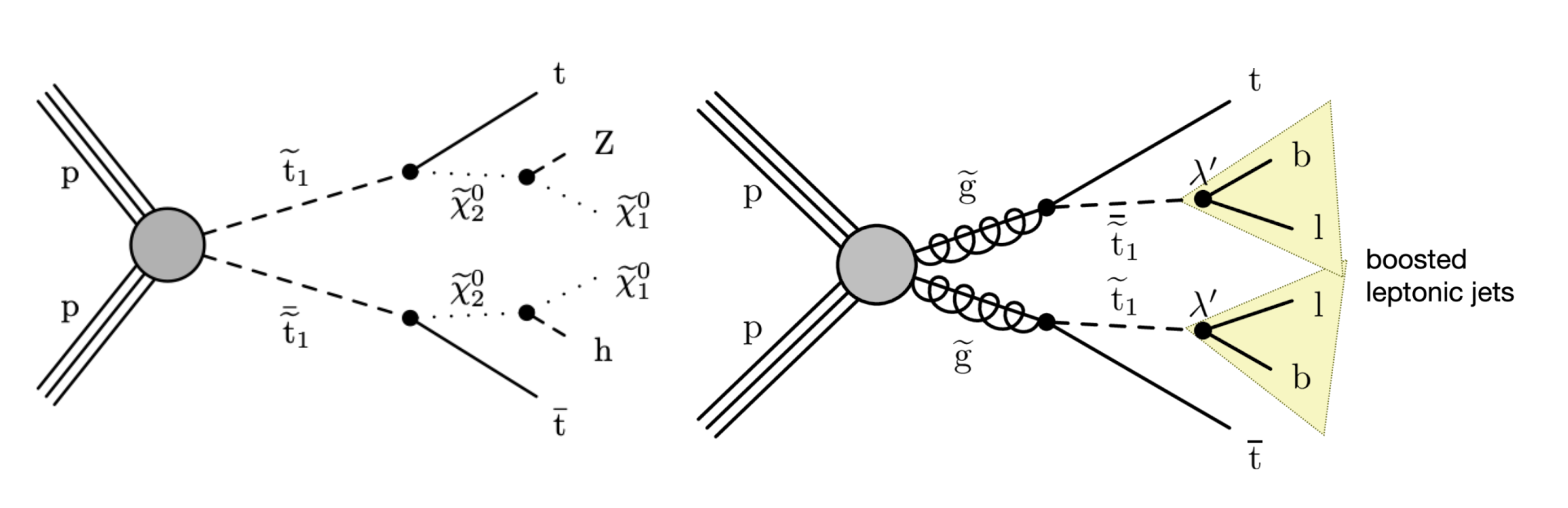
Figure 1: Two SUSY processes that can lead to boosted objects for large mass splittings. The model on the right has RPV top squarks that decay into a b quark and a lepton. The RPV top squarks can be reconstructed as boosted leptonic jets.
Overall, the analysis considered three channels, with zero leptons, with one isolated lepton, and with one or more nonisolated leptons, and examined 25 unique and statistically independent final states with varying combinations of boosted object types, jets, b jets, and leptons. Signal discrimination in each search region relied on the razor kinematic variables, which use either the longitudinal or transverse components of the observed objects to estimate the mass relations between the signal particles. SUSY signals would thus appear as a clear bump above the smoothly falling background from standard model processes.
Figure 2 shows the distributions of data and estimated backgrounds across all signal regions, binned in razor variables, and the effect of uncertainties. The statistical fit to data showed no significant deviations from standard model predictions. It also displays selected mass points from eight simplified SUSY models, defined by idealised production and decay mechanisms involving only two or three SUSY particles. Different SUSY signals populate different regions of the analysis, illustrating the complementarity of the 25 signal regions.

Figure 2: Distributions of data, estimated backgrounds, and selected signal models in the hadronic (left) and leptonic (right) search regions.
The agreement was used to set stringent upper limits on superparticle production rates and masses in the eight signal models, including two processes with RPV top squarks and RPV neutralinos so far not interpreted by LHC searches. Figure 3 shows the exclusion limits for the top squark production scenario and RPV top squark scenario, whose diagrams were shown above.

Figure 3: Exclusion limits on the two signal models shown in Figure 1.
But the journey of razor boost is not over. The 25 final states examined here provide the breadth necessary to move beyond simplified models and interpret the results within the context of complete SUSY frameworks, which encompass the full spectrum of superparticles and a realistic range of production and decay modes. Different final states are sensitive to different decay channels of a given superparticle, and their combined impact will yield stronger constraints on such models. This broader interpretation is now underway, using a 19-parameter representation of the minimal supersymmetric standard model known as the phenomenological MSSM. It will extend the reach of this search across the wider SUSY landscape, helping to clarify our picture of this compelling theory.
