Uniting Leptogeneses

With the discovery of the Higgs boson, particle physics has reached an era of unprecedented success. Almost all phenomena in nature can in principle be explained with known particles of the Standard Model (SM). Some puzzles still remain unsolved, like the origin of observed matter-antimatter asymmetry of the Universe (BAU), the existence of surprisingly small neutrino masses, and the nature of dark matter (DM). In this article we will argue that a common solution to at least two of these problems is within reach of near future experiments, at either the high intensity (beam dump experiments such as SHiP), or at the high energy frontiers (LHC and future colliders such as FCC-ee).
All fermions in the SM obtain their masses via the Higgs field, which couples the left and right handed chiral partners. However, among the neutrinos, we have only observed the left-handed states. This leads to an exciting possibility, that right-handed neutrinos could exist and play a role in neutrino mass generation.
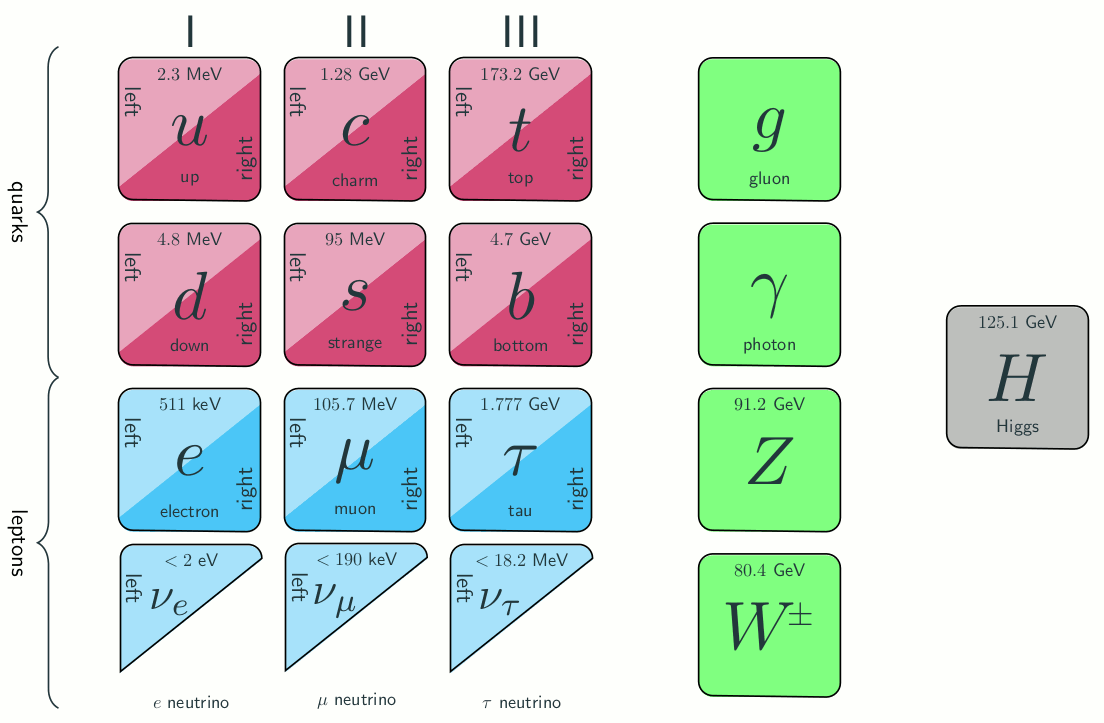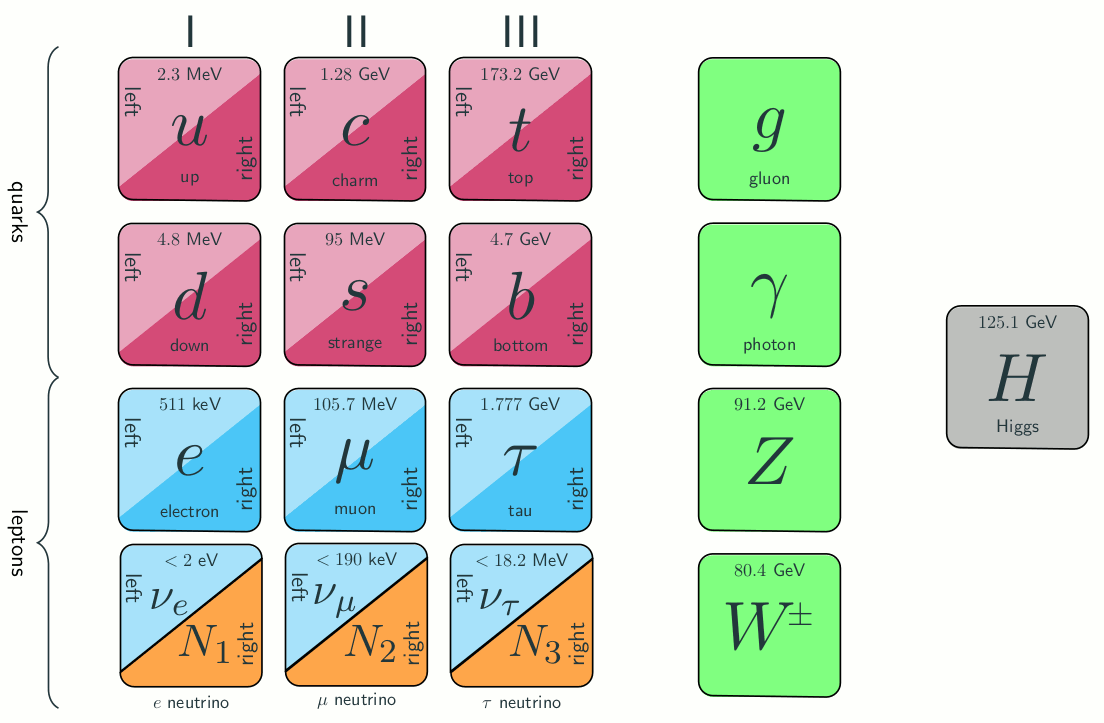
Figure 1: Particle content of the SM and its extension by three right-handed neutrinos.
If they exist, these right-handed neutrinos are different from the other particles in the SM, as they are singlets with respect to the SM gauge group. As such, they can have an additional Majorana mass, not related to the Higgs field. The only interactions the right-handed neutrinos participate in are the Yukawa interactions with the Higgs field and the left-handed neutrinos. Once the electroweak symmetry is broken, and the Higgs field obtains its vacuum expectation value, the left- and right-handed neutrinos mix. This mixing has important consequences for both sets of neutrinos. The left-handed neutrinos obtain parametrically small masses via the celebrated seesaw formula.

where Y and MN symbolize the Yukawa couplings and Majorana masses of the heavy neutrinos N respectively, and v is the vacuum expectation value of the Higgs field. As for the heavy neutrinos, they start to interact with the W and Z bosons. We should note that the seesaw formula does not fix the masses of the heavy neutrinos, which could be as small as a fraction of eV, or as large as 1015 GeV. If the masses of the heavy neutrios are close to the electroweak scale, they could be produced at experiments. Following the Particle Data Group, we will call these particles Heavy Neutral Leptons (HNLs).
But the tiny neutrino masses are not the only problem HNLs can solve — they could also provide a candidate for a DM particle and explain the observed BAU, as it the case in the Neutrino Minimal Standard Model (νMSM)1. For every photon there are approximately 6 × 10−10 baryons present in the Universe. This tiny ratio indicates that there was an asymmetry between baryons and antibaryons in the very early universe. Without this asymmetry, all baryons would have annihilated with antibaryons leaving a pretty boring Universe filled with photons and neutrinos. For the observed BAU to be generated, the three famous Sakharov conditions need to be met:
1) Efficient baryon number violation
2) Sizeable C and CP violation
3) Substantial deviation from thermal equilibrium
In the SM, nonperturbative sphaleron processes fulfil condition 1), but the CP asymmetry in the quark sector is too small to satisfy 2). Also, there are no significant deviations from equilibrium in the course of thermal history of the Universe: with the measured Higgs mass of 125 GeV, the transition from the symmetric to the Higgs phase in the early Universe is a smooth crossover. As a result, the SM cannot explain the baryon asymmetry.
Heavy Majorana neutrinos can provide both CP violation via the complex Yukawa couplings2, as well as a deviation from equilibrium. The evolution of the Universe can be summarised as follows. The concentration of the HNLs is negligibly small after inflation and they are created in the course of evolution in reactions with ordinary leptons and Higgses. Depending on heavy neutrino masses (and therefore their Yukawa couplings, since they are related by the seesaw formula above), two evolution patterns are possible: 1) large MN and large Y ; 2) small MN and Y . We depict these two possibilities in Figure 2.

Figure 2: Schematic illustration of how the heavy neutrino number density normalized to photon number density (blue) changes with time in the early universe. The equilibrium abundance is shown (orange) for comparison and the deviation from equilibrium is highlighted. The purple vertical line shows the moment when sphalerons become inefficient and the lepton asymmetry cannot be transferred to the baryon sector. The freeze-out and freeze-in mechanisms differ by the position of this purple line.
In the case of large masses and Yukawa couplings, the matter-antimatter asymmetry can be generated in the decays of heavy neutrinos (c.f. Fig. 3). The heavy neutrinos will decay into leptons and antileptons with different probabilities due to quantum corrections. This leads to an overall asymmetry in the abundances of leptons and antileptons in the Universe. The process of creating a lepton asymmetry is known as leptogenesis.
Figure 3: A typical decay of a heavy neutrino. The decay asymmetry is generated through the interference of the tree level process with the vertex and wave function contributions.
This lepton asymmetry can turn into a baryon asymmetry through sphaleron processes, which can convert baryons to leptons and vice versa. These processes were present when the Universe was only 3×10−11 seconds old, and very hot, as they are only efficient at temperatures T > Tsph ≈ 130 GeV ≈ 1015 K.
If the masses of the heavy neutrinos are hierarchical, they would have to be extremely heavy, MN > 109 GeV. However, if the difference in mass between two heavy neutrinos is tiny, their masses can be much lower, as the decay asymmetry becomes resonantly enhanced in a process known as resonant leptogenesis
Finally, to satisfy the third Sakharov condition, the decays of the HNLs have to happen out of thermal equilibrium. This deviation from thermal equilibrium caused by the temperature dropping below the heavy neutrino mass is known as freeze-out (i.e. HNLs are in thermal equilibrium at high temperature and then they go out of equilibrium). This is depicted in the left panel of Figure 2.
In fact, freeze-out is not the only way to deviate from equilibrium, a significant deviation from equilibrium is also realized when they are produced, during freeze-in (i.e the HNLs are out of thermal equilibrium at high temperature and they enter in it at lower temperature). This is shown in the right panel of Figure 2.
Freeze-in leptogenesis was primarily studied in the context of GeV-scale HNLs. Light HNLs typically have smaller Yukawa couplings, and therefore — slower interactions. The slowness of interactions allows the HNLs to remain out of equilibrium for a longer time, and thus satisfy the out-of-equilibrium condition. The leptonic asymmetries are generated in a mechanism quite similar to known neutral particle (e.g. kaon) oscillations. The HNLs are produced in the interaction basis, like K0 mesons are produced in strong interactions, which in general does not coincide with their mass basis, like KL, KS mixtures of K0 and anti-K0 . This misalignment causes CP-violating oscillations, which can then lead to lepton, and therefore baryon asymmetries
It was expected that freeze out leptogenesis is only operative at MN ≩ 130 GeV because N should decay at T > Tsph, see the left panel of Figure 2. Since freeze-in leptogenesis crucially depends on a deviation from equilibrium, it was in turn expected that it is only possible if the HNL masses are below to the W-boson mass, MN ≲ 80 GeV, when more equilibration channels (such as N → Zν) open up.
Thus, one could come to the conclusion that the two mechanisms are different, or at least have disconnected parameter spaces. As we have shown in our recent paper, this turns out not to be the case, the two mechanisms overlap, and their parameter spaces are continuously connected. In particular, the freeze-in leptogenesis parameter space extends to TeV-scale HNL masses and beyond, while the freeze-out mechanism extends down to the GeV scale. We identified several reasons for this overlap. One of the most important effects is that the interactions which bring the HNLs into equilibrium do not always erase the asymmetries in a particular flavor that were created earlier. This is especially true if the HNLs interact with one of the flavors much less than with the other flavors — i.e. the HNL couplings to the different flavors are hierarchical. The size of this coupling is largely determined by the phases in the light neutrino mass matrix — the Dirac CP violating phase, and by the Majorana phase. Another important factor preventing large washout is that lepton number is approximately conserved when the HNL mass difference is small compared to their lifetime. This is often the case in freeze-out leptogenesis, especially if the mixing angles are large. Finally, it is also important to note that the freeze-out of lepton number is not an instantaneous process and starts even before MN > T, insofar that freeze-out leptogenesis remains possible for MN ∼ few GeV.
Figure 4: Within the white regions it is possible to reproduce the observed value of the BAU and explain the neutrino masses. For comparison we also show the expected sensitivities of SHiP (green), HL-LHC (red) and FCC-ee (blue). The plot is for the normal hierarchy (NH) of active neutrinos.
Perhaps surprisingly, this indicates that, just as there is no preferred HNL mass scale for the seesaw mechanism — there is no preferred HNL mass scale from leptogenesis, all masses above ∼ 100 MeV are allowed. This theoretical result has important consequences for existing and near-future experiments. We are at an exciting point in history: the planned future experiments such as SHiP and FCC-ee in the Z resonance mode have chances to uncover soon the origin of neutrino masses and baryon asymmetry of the Universe.
Notes
1. Below we only discuss the latter. For this end we drop the lightest of the HNLs — N1, which is a dark matter candidate and is irrelevant for baryogenesis and neutrino mass generation as it effectively decouples from the SM particles.
2. Similarly, it is exactly the complex quark Yukawa couplings that are the origin of CP violation in the quark sector
