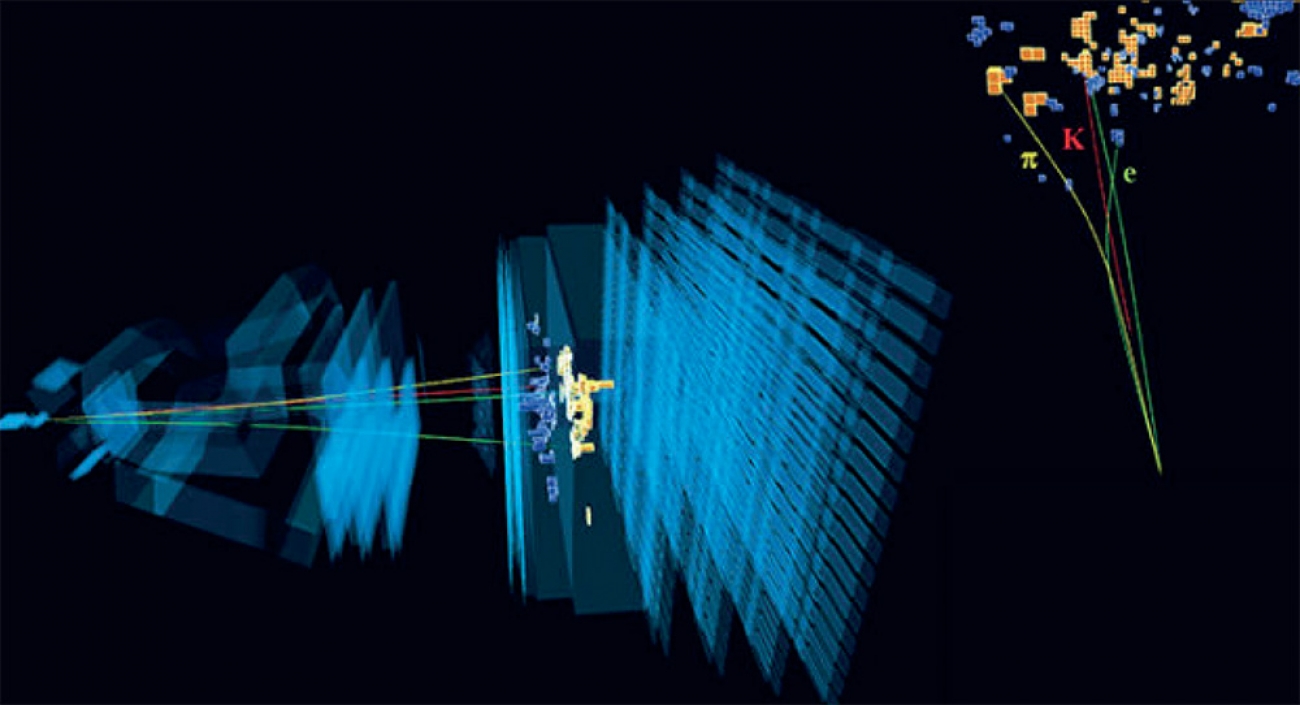
The crown jewel of particle physics, the Standard Model (SM), has withstood numerous experimental trials. However, there are still some observations it cannot explain. Examples such as dark matter and the matter-antimatter imbalance in the Universe come to mind. The SM may be extended, by including additional particles and interactions, so as to explain such phenomena. These new particles and interactions are collectively referred to as “new physics” (NP), and the results covered by this article provide a promising lead for their discovery.

Flavour anomalies

In the past decade, a pattern has been emerging in the study of b-quark decays with leptons in the final state. They are collectively referred to as “flavour anomalies”, and they typically feature tensions at the level of 2–3 standard deviations between experimental results and SM predictions. As such, individual anomalies are not sufficiently significant to claim discovery of NP. However, the anomalies are often treated collectively in an Effective Field Theory (EFT) framework, whereby short distance contributions are separated from their long distance counterparts. This is similar to the 4-point approximation used to describe beta decay, where the process is observed at long enough distances to regard the W boson propagator as point-like.

The EFT approach leads to the formulation of an effective Lagrangian, L_eff = Σ_i C_iO_i , where large energy-scale effects are encoded in the so-called Wilson coefficients C_i , and small energy-scale contributions are accounted for by the Wilson operators O_i . Given the absence of direct discoveries at the LHC, NP is assumed to be characterised by large (above TeV) energy scales. The anomalous flavour observables could then be impacted indirectly, since NP particles may manifest themselves virtually. From an EFT prespective, this would lead to values of the C_i coefficients that differ from the SM values.

Two examples of EFT analyses of flavour anomalies are shown in Figure 1 [1-3]. In the plot on the left-hand side, the 1σ and 2σ confidence levels for the best-fit point for the considered anomalies are shown in red. On the right-hand side, the best-fit 1σ, 2σ, and 3σ confidence levels are shown in green. The two analyses make different assumptions on the presence of NP in the coefficients C_i (as shown by the axes), however they both find that the flavour anomalies prefer C_i values that are significantly different from the ones predicted by the SM (the origin in each plot).

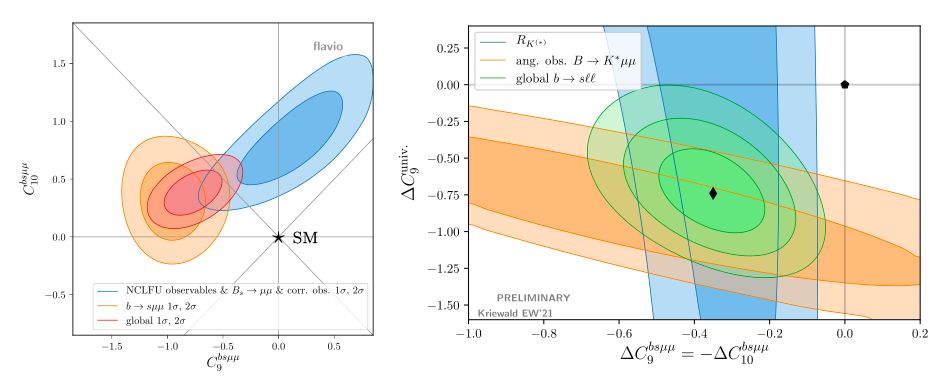
Figure 1: Examples of EFT fits to anomalous flavour observables [1-3], under different NP scenarios. Blue confidence regions show values preferred by flavour anomalies that are theoretically cleaner compared to other anomalies, whose preferred values are depicted in orange. Confidence regions preferred by all considered flavour anomalies are shown in red and green.

Clean observables

There are several types of anomalous flavour observables, such as differential branching fractions and angular coefficients. They are predicted in the SM with various degrees of precision, and so particularly important are the flavour anomalies that are theoretically clean. Recently, at the Electroweak session of the Moriond 2021 conference, the LHCb collaboration has presented the most precise individual measurements to date of two such theoretically-clean anomalous observables. The first one is the ratio of branching fractions R_K = B(B^± → K^±μ⁺μ⁻) / B(B^± → K^±e⁺e⁻) [4]. The second one is the branching fraction of B_s⁰ → μ⁺μ⁻ , including a search for B⁰ → μ⁺μ⁻ and B_s⁰ → μ⁺μ⁻γ [5,6]. The processes involved are examples of Flavour Changing Neutral Currents (FCNCs), which are forbidden at tree-level in the SM. As a result, the leading-order Feynman diagrams contain loops, as exemplified by Figure 2. The loops introduce additional vertices that make these processes rare.

The branching fraction of B_s⁰ → μ⁺μ⁻ is predicted by the SM with subpercent precision, thanks to the purely-leptonic final state: (B_s⁰ → μ⁺μ⁻) = (3.66 ± 0.14) × 10⁻⁹ [7]. The two B^± → K^±ℓ⁺ℓ⁻ processes upon which R_K is built have branching fractions of O(10⁻⁶) [8]. They differ only by the leptons in the final state, which means R_K can be predicted accurately by virtue of Lepton Flavour Universality (LFU). This is an accidental symmetry of the SM, whereby the different lepton flavours couple in the same way to vector bosons. As a result, R_K is predicted to be approximately 1, with small deviations induced by phase space differences and QED corrections [9,10].

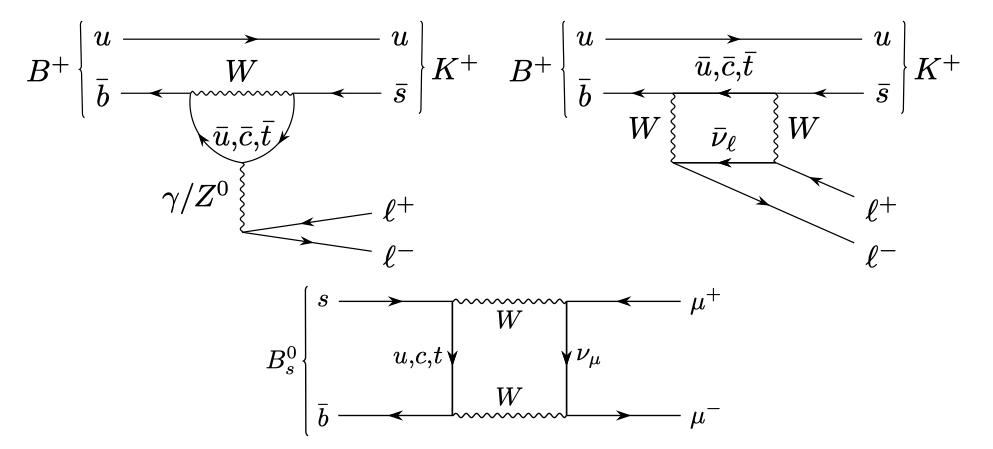
Figure 2: Examples of lowest-order Feynman diagrams allowed in the SM for B⁺ → K⁺ℓ⁺ℓ⁻ (top) and B_s⁰ → μ⁺μ⁻ (bottom). Since FCNCs are forbidden at tree-level, each of these diagrams contains a loop.

Despite the unambiguous SM predictions, experimental results on B_(s) → μ⁺μ⁻and R_K were exhibiting tensions above 2σ before the Moriond 2021 conference, as shown in Figure 3. The LHCb measurements shown here used 5 fb⁻¹ of proton-proton collision data, corresponding to approximately half of the currently available dataset. Given the bigger picture in the context of the flavour anomalies, updates to B_(s) → μ⁺μ⁻ and R_K based on the full LHCb data set are crucial to better understanding whether there is NP in rare b-decays.

Figure 3: Experimental status of B_s⁰ → μ⁺μ⁻ (left) and R_K (right) before the Moriond 2021 conference. Shown on the left are 1–5σ confidence regions (shades of blue) for the combination [11] of B_s⁰ → μ⁺μ⁻ and B⁰ → μ⁺μ⁻ measurements from ATLAS [12], CMS [13], and LHCb [14], alongside the SM prediction (red). Shown on the right are results on R_K from LHCb [15,16] (black and grey), BaBar [17] (green), and Belle [18] (blue); the latter has since been updated [19]. The SM prediction is shown as a dashed line at R_K = 1.

Measurement of R_K

Highly anticipated updates to the R_K and B_(s) → μ⁺μ⁻ measurements, now including the full dataset of 9 fb⁻¹ of proton-proton collisions collected by LHCb, were presented at the Moriond 2021 conference. At the core of the R_K measurement is the comparison of selection efficiencies between electrons and muons. The masses of the two leptons differ by two orders of mangitude, which leads to them interacting differently with the detector. Muons traverse the LHCb detector almost undisturbed, before finally being stopped by the muon stations. However, electrons are subject to significant loss of energy to bremsstrahlung radiation, leading to worse momentum and mass resolution compared to muons. In order to suppress detection effects that are systematically different between the two lepton flavours, R_K is measured as a double ratio:

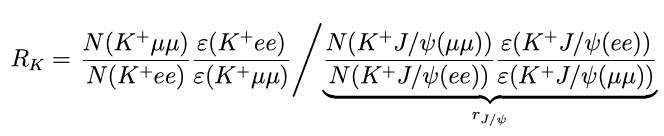
where N(X) and ε(X) represent respectively the yields and efficiencies of selecting the decay of a B⁺ meson into X. The J/ψ modes upon which the single ratio r_J/ψ is built are used to calibrate efficiencies and conduct cross-checks. These modes are characterised by high statistics, and are known to respect LFU [8]. In addition, the B^± → K^±J/ψ (ℓ⁺ℓ⁻) (control) channels are kinematically similar to the B^± → K^±ℓ⁺ℓ⁻ (rare) channels, and so the data are selected with identical requirements for both. The only exceptions are the cut on the dilepton invariant mass squared, q², and the reconstructed B mass. The control data are selected using a q² window around the J/ψ resonance, whilst the B^± → K^±ℓ⁺ℓ⁻ candidates are required to have q² between 1.1 and 6.0 GeV². This q² window is chosen to prevent contamination from resonances such as φ(1020) (at low q²) and J/ψ (at high q²).

Several cross-checks are performed to ensure the selection efficiencies are well understood. Among these checks are the ratios r_J/ψ and R_ψ(2S) . Like R_K , the latter is a double ratio with respect to r_J/ψ, the difference being that the numerator comes from the ψ(2S) resonance. The ratios are found to be r_J/ψ = 0.981 ± 0.020 (stat + syst), and R_ψ(2S) = 0.997 ± 0.011 (stat + syst). Both are compatible with the LFU expectation of 1. This confirms that the efficiencies are valid across q², and that systematic effects successfully cancel out in the double ratio.

The value of R_K is extracted from an unbinned maximum likelihood fit to the selected     B^± → K^±e⁺e⁻ and B^± → K^±μ⁺μ⁻ data. The different mass resolutions lead to different background components in the fit model, as shown in Figure 4. The result for R_K [4] is:

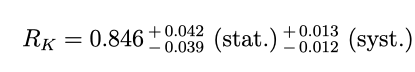
As expected, the uncertainty on the result is dominated by the statistical component, rather than the systematic one. The dominant systematic effect is the choice of the fit model, which contributes by around 1%. By comparison, effects induced by the calculation of efficiencies are reduced to the permille level by the double ratio

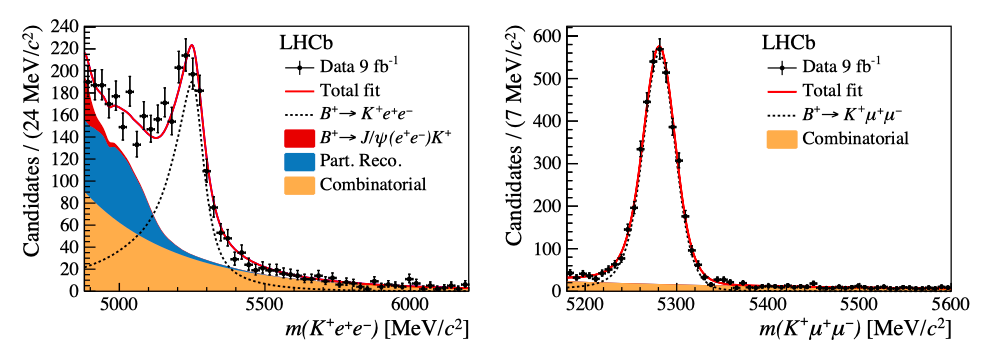
Figure 4: Fit projections for B^± → K^±e⁺e⁻ (left) and B^± → K^±μ⁺μ⁻ (right) candidates. The resolutions and background components differ as a result of the different behaviour of electrons and muons as they traverse the LHCb detector.

Branching fractions of B_(s)⁰ → µ⁺µ⁻(γ)

Thanks to the excellent mass resolution of muons, the signature of B_(s) → μ⁺μ⁻ decays is very clean. It consists of a pair of oppositely charged muons that have an invariant mass around mass of the B_(s) , and that form a vertex that’s significantly displaced from the interaction point. The branching fraction of the signal decays are extracted from an unbinned maximum likelihood fit to the dimuon invariant mass and are measured relatively to two normalisation channels, B^± → K^±J/ψ (μ⁺μ⁻) and B⁰ → K⁺π⁻ which both share similarities with the signal. The former is characterised by similar particle identification and trigger performance, and the latter has similar kinematics. The branching fraction is written as:

where N_sig and N_norm are the yields of the signal and normalisation channels, respectively. The corresponding efficiencies and fragmentation fractions are denoted by ε_norm(sig) and f_norm(sig) respectively. LHCb provided a measurement for the latter in [20]. In order to maximise sensitivity to the signal, a boosted decision tree (BDT) is used to separate signal and background

The fit for the B_(s) → μ⁺μ⁻ yields is performed simultaneously on subsets of the data separated by BDT output. The left-hand side plot of Figure 5 shows the expected relative yield of B_(s) → μ⁺μ⁻,in bins of BDT score, as estimated using two different methods. The red distribution uses a BDT calibration based on the control channel B⁰ → K⁺π⁻, as done in the previous LHCb analysis [14]. The black histogram uses calibrated B_(s) → μ⁺μ⁻ simulation. The two methods yield compatible results, and the new BDT calibration method significantly improves the precision on the expected relative yield. This is important because it directly improves the total uncertainty of the branching fraction measurement.

Figure 5: Left: expected distribution of the relative signal yield, as a function of the BDT score. Right: invariant-mass distribution of B_(s) → μ⁺μ⁻ candidates with BDT score above 0.5. The total fit model is shown in blue, alongside the individual components that represent signal and background.

The branching fraction of B_(s) → μ⁺μ⁻ is obtained from a fit to the invariant mass of the dimuon system, which is shown on the right-hand side of Figure 5. In addition to the B_s⁰→ μ⁺μ⁻ signal, the fit model contains contributions from B⁰→ μ⁺μ⁻and B_s⁰→ μ⁺μ⁻γ. These two components are compatible with the background-only hypothesis, and so upper limits are set on their corresponding branching fractions. In summary, the results are:

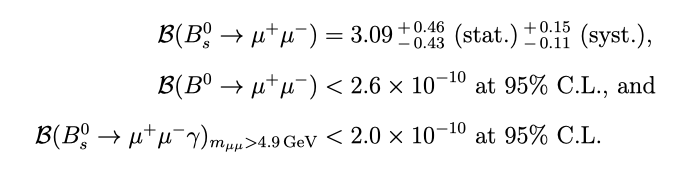
Like R_K, the measurement of B(B_s⁰→ μ⁺μ⁻) is dominated by statistics. The systematic uncertainty is largely due to the uncertainty on f_s/f_d. The measured values are compatible with the previous results, as well as with the SM predictions, at the 1σ level.

Status and prospects

The updaded results on R_K and the B_(s) → μ⁺μ⁻ branching fractions are summarised in Figure 6. While the SM prediction for B(B_(s) → μ⁺μ⁻) still lies within the 95% C.L. of the experimental result, the central value is relatively unchanged with respect to the previous LHCb measurement. The same is true for the central value of the R_K result: thanks to the increase in statistics with respect to the previous measurement, it now exhibits 3.1σ tension with respect to the value predicted by the SM [9,10]. Therefore, this R_K measurement represents the first evidence for the violation of LFU in B^± → K^±ℓ⁺ℓ⁻ decays.

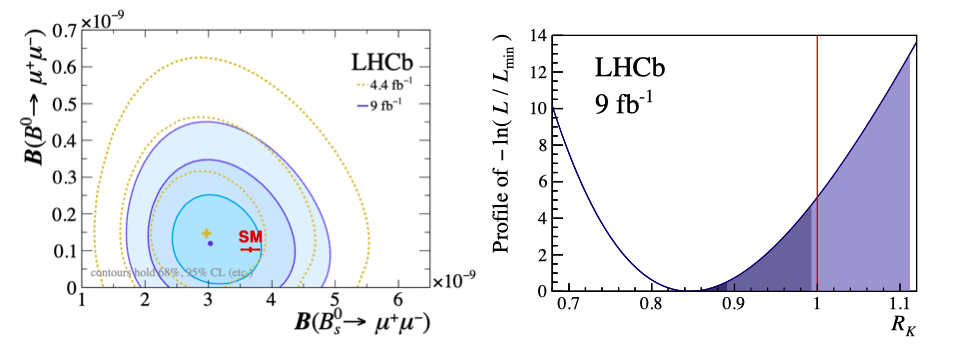
 Figure 6: Experimental status of B_(s) → μ⁺μ⁻ (left) and R_K (right) after the Moriond 2021 conference. Shown on the left are 1–3σ confidence regions (shades of blue) of B_s⁰→ μ⁺μ⁻ and B⁰→ μ⁺μ⁻ measurements from LHCb [5,6], alongside the SM prediction (red). Shown on the right is the likelihood function from the fit to B^± → K^±ℓ⁺ℓ⁻ candidates, profiled in R_K . The extent of the dark, medium and light blue regions show the values allowed for R_K at the 1σ, 3σ, and 5σ levels, respectively. The SM prediction is shown as a solid line at   R_K = 1.

Since all presented measurements are dominated by the statistical uncertainty, future updates are crucial to the better understanding of the flavour puzzle. In Table 1 are summarised the projected improvements on the precision of the measurements of R_K and B_(s) → μ⁺μ⁻ the following years of data taking. The limiting factor in the precision of R_K is the yield of the electron mode, which, assuming the same detector performance as in    Run 1, would increase more than 40 times at the end of Run 4. This would bring the statistical uncertainty on R_K on par with the QED corrections. The error projection on   B_s⁰→ μ⁺μ⁻ at future upgrades depends on the assumptions made on the systematic uncertainties, particularly f_s/f_d . A conservative estimate of 4% would imply an uncertainty of B(B_s⁰→ μ⁺μ⁻) to be approximately 0.30 × 10⁻⁹ with 23 fb⁻¹ and 0.16 × 10⁻⁹ with    300 fb⁻¹ of data [21].

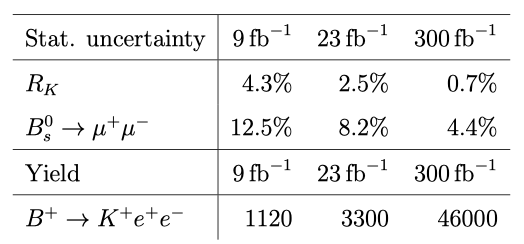
Table 1: Extrapolation, based on Run 1 results, of statistical uncertainties on R_K, B(B_s⁰→ μ⁺μ⁻) (expressed in units of their SM predictions), and the expected electron-mode yield at the end of future detector upgrades. The b-quark production cross-section is assumed to scale linearly with centre-of-mass energy, and the detector performance is assumed to be unchanged with respect to Run 1. Adapted from Ref. [21].

The EFT interpretation in terms of shifts in muonic Wilson Coefficients ∆C_i^μ from their SM value, in light of the new results of R_K and B_(s) → μ⁺μ⁻ , is updated in Figure 7 [22]. In the  plot on the left, the light orange horizontal band highlights the interval of ∆C₁₀^μpreferred by the combined ATLAS, CMS, and updated LHCb measurements of B(B_(s) → μ⁺μ⁻). The elongated purple shape marks the regions of ∆C₉^μ and ∆C₁₀^μcompatible with the measured values of R_K and R_K* [23]. Thanks to their different sensitivity to the ∆C_i^μ the combination of these two measurement forms the unfilled contours, which are significantly displaced from the SM point. In the plot on the right, the contribution from other b^± → s^±ℓ⁺ℓ⁻ observables, such as the angular ones in the B → K^*μ⁺μ⁻ system [24], is included in the ∆C_i fit. While the clean observables presented in this article are insensitive to a flavour-universal shift in C₉ , ∆C₉^U, the observables characterised by less precise theoretical predictions are nonetheless able to provide substantial sensitivity to potential shifts in the muonic Wilson coefficients, when combined with R_K and B_(s) → μ⁺μ⁻.

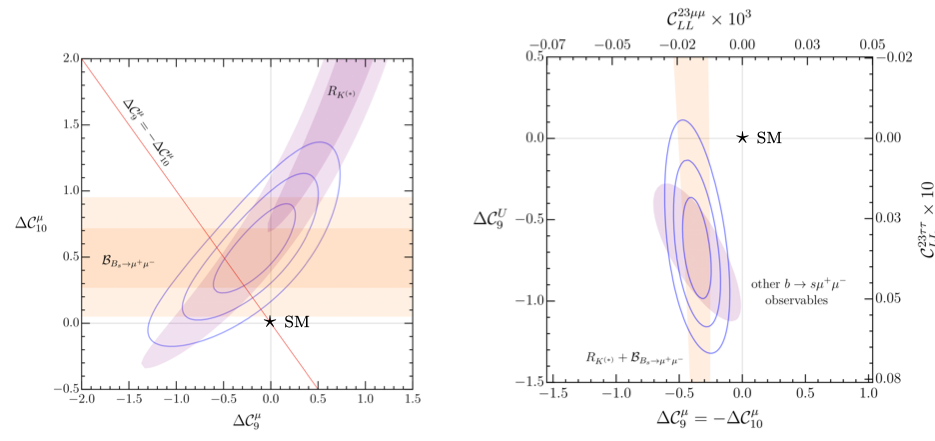
Figure 7: EFT constraints from the b^± → s^±ℓ⁺ℓ⁻ anomalies [22]. Left: Results of the  two-dimensional fit to muonic ∆C₉^μ and ∆C₁₀^μusing clean observables only (1σ, 2σ and 3σ intervals). Also shown are the 1σ and 2σ intervals from R_K , R_K* , and B_s⁰→ μ⁺μ⁻ , the latter under the hypothesis ∆C₉^U = 0. Right: Results of the two-dimensional fit to ∆C₁₀^μ = −∆C₉^μ and universal ∆C₉^U using all b^± → s^±ℓ⁺ℓ⁻ observables. The vertical band shows the result using clean observables only (1σ interval), while the ellipse denotes the contribution of all the other observables, estimated using Flavio [25] (1σ interval).

In light of the recent results from LHCb, the flavour puzzle has become even more intriguing. LHCb will continue to improve the precision on its anomalous flavour measurements, whilst also investigating related observables that could provide complementary information. Verification from other experiments, such as Belle II, is expected in the near future, so exciting times lay ahead of the particle physics community!

Further Reading

[1] W. Altmannshofer and P. Stangl, New Physics in Rare B Decays after Moriond 2021, arXiv:2103.13370.1

[2]  M. Algueró et al., b → sll global fits after Moriond 2021 results, in 55th Rencontres de Moriond on QCD and High Energy Interactions, arXiv:2104.08921.

[3] C. Hati, J. Kriewald, J. Orloff, and A. M. Teixeira, The fate of vector leptoquarks: the impact of future flavour data, arXiv:2012.05883. 

[4] LHCb collaboration, R. Aaij et al., Test of lepton universality in beauty-quark decays, arXiv:2103.11769, Submitted to Nature Physics. 

[5] LHCb collaboration, R. Aaij et al., Analysis of neutral B-meson decays into two muons, arXiv:2108.09284, submitted to PRL.

[6] LHCb collaboration, R. Aaij et al., Measurement of the B_s⁰→ μ⁺μ⁻  decay properties and search for the B⁰→ μ⁺μ⁻ and B_s⁰→ μ⁺μ⁻γ decays, arXiv:2108.09283, submitted to PRD.2021-008.

[7] M. Beneke, C. Bobeth, and R. Szafron, Power-enhanced leading-logarithmic QED corrections to B_q→ μ⁺μ⁻ , JHEP 10 (2019) 232, arXiv:1908.07011.

[8] Particle Data Group, P. A. Zyla et al., Review of Particle Physics, PTEP 2020 (2020), no. 8 083C01.

[9] M. Bordone, G. Isidori, and A. Pattori, On the Standard Model predictions for R K and R K ∗ , Eur. Phys. J. C76 (2016), no. 8 440, arXiv:1605.07633.

[10] G. Isidori, S. Nabeebaccus, and R. Zwicky, QED corrections in B^± → K^±ℓ⁺ℓ⁻ at the double-differential level, JHEP 12 (2020) 104, arXiv:2009.00929.

[11] LHCb collaboration, Combination of the ATLAS, CMS and LHCb results on the  B_(s) → μ⁺μ⁻ decays, LHCb-CONF-2020-002. ATLAS-CONF-2020-049, CMS PAS  BPH-20-003, LHCb-CONF-2020-002.

[12] ATLAS, M. Aaboud et al., Study of the rare decays of B_s⁰ and B⁰ mesons into muon pairs using data collected during 2015 and 2016 with the ATLAS detector, JHEP 04 (2019) 098, arXiv:1812.03017.

[13] CMS, A. M. Sirunyan et al., Measurement of properties of B_s⁰→ μ⁺μ⁻ decays and search for B⁰→ μ⁺μ⁻ with the CMS experiment, JHEP 04 (2020) 188, arXiv:1910.12127.

[14] LHCb collaboration, R. Aaij et al., Measurement of the B_s⁰→ μ⁺μ⁻ branching fraction and effective lifetime and search for B⁰→ μ⁺μ⁻ decays, Phys. Rev. Lett. 118 (2017) 191801, arXiv:1703.05747.

[15] LHCb collaboration, R. Aaij et al., Search for lepton-universality violation in B^± → K^±ℓ⁺ℓ⁻ decays, Phys. Rev. Lett. 122 (2019) 191801, arXiv:1903.09252.

[16] LHCb collaboration, R. Aaij et al., Test of lepton universality using B^± → K^±ℓ⁺ℓ⁻ decays, Phys. Rev. Lett. 113 (2014) 151601, arXiv:1406.6482.

[17] BaBar Collaboration, Measurement of Branching Fractions and Rate Asymmetries in the Rare Decays B→ K^(*)ℓ⁺ℓ⁻, Phys. Rev. D86 (2012) 032012.

[18] Belle collaboration, Measurement of the Differential Branching Fraction and Forward-Backward Asymmetry for B → K^(*)ℓ⁺ℓ⁻, Phys. Rev. D103 (2009) 12.

[19] Belle, S. Choudhury et al., Test of lepton flavor universality and search for lepton flavor violation in B → Kℓℓ decays, JHEP 03 (2021) 105, arXiv:1908.01848.

[20] LHCb, R. Aaij et al., Precise measurement of the f_s/f_d ratio of fragmentation fractions and of B_s⁰ decay branching fractions, arXiv:2103.06810.

[21] LHCb collaboration, Physics case for an LHCb Upgrade II — Opportunities in flavour physics, and beyond, in the HL-LHC era, arXiv:1808.08865.

[22] C. Cornella et al., Reading the footprints of the B-meson flavor anomalies, arXiv:2103.16558.

[23] LHCb, R. Aaij et al., Test of lepton universality with B⁰ → K^*0ℓ⁺ℓ⁻ decays, JHEP 08 (2017) 055, arXiv:1705.05802.

[24] LHCb, R. Aaij et al., Measurement of CP -Averaged Observables in the B⁰ → K^∗0μ⁺μ⁻ Decay, Phys. Rev. Lett. 125 (2020), no. 1 011802, arXiv:2003.04831.

[25] D. M. Straub, Fllavio: a Python package for flavour and precision phenomenology in the Standard Model and beyond, arXiv:1810.08132.