Over the past century, a whole zoo of particles has been discovered and their interactions have been investigated. This led to a puzzling mystery; on the one hand we discovered a property of Nature, known as electro-weak symmetry, which gave a unified explanation of radioactive decay and electromagnetism; on the other hand, almost all particles possess mass, which seems forbidden by this very symmetry. An elegant solution to this paradox was to propose the existence of a new field, the Higgs field, that has just the right properties so that it is energetically favourable to have a non-zero value everywhere, breaking electro-weak symmetry. Then, particles can acquire a mass, depending on how strongly they interact with this field. Half a century after this mechanism was proposed, one of the most ambitious scientific endeavours in history, the CERN Large Hadron Collider (LHC), discovered the existence of this Higgs field.

It has long been predicted that in the extreme heat of the very early Universe, the Higgs field will undergo radical changes. At very high temperature, it is energetically preferred for the Higgs field to be zero everywhere. This implies that electro-weak symmetry is exactly obeyed by Nature, and the Higgs field no longer provides mass to matter. Within a hundred picoseconds of the Big Bang, the Universe cools to the point where electro-weak symmetry is broken.

Exactly how electro-weak symmetry breaking occurs is currently a mystery. We have not examined the Higgs field precisely enough to even determine whether the transition proceeds smoothly, or through the nucleation and coalescence of bubbles — that is, whether there was a cosmological first order electro-weak phase transition. The Standard Model of particle physics (SM) predicts a smooth transition (a cross-over), but the hierarchy between the Planck (the scale at which gravity becomes strong) and electro-weak scale is unnatural, and there are many outstanding issues that predict, or even require, a first order electro-weak phase transition.

New states at the electro-weak scale can easily alter the whole picture. In particular, they can modify the shape of the Higgs field’s potential, as well as how it evolves with temperature. If a barrier formed between the true and false vacua, as shown in the animation below, then electro-weak symmetry breaking will not have been homogeneous as the SM predicts, but the spectacular process of a cosmic first-order phase transition through the coalescence of vacuum bubbles.

Figure 1: A schematic animation of the evolution of the Higgs field’s (φ) potential, V(φ), for a first-order transition. As the Universe cools down, a second minimum appears away from the origin. The second minimum then becomes as deep as the one at the origin at the critical temperature, beyond which tunneling becomes viable, allowing the formation of vacuum bubbles.

Any new physics that modifies the SM prediction of a smooth cross-over cannot lie at an arbitrarily high scale, as it has to modify physics at the weak scale. This turns the nature of cosmological electro-weak symmetry breaking into a key question of next-generation collider experiments.

If the Higgs field really did cause the Universe to “boil” via bubbles, this could answer one of the most fundamental questions of our existence: Why is there so much more matter than antimatter? The necessary, so-called, “sphaleron processes” are suppressed in the low-temperature broken phase, but efficiently violate the conservation of baryon (i.e. matter) number in the symmetric phase. If there are Charge-Parity (CP)-violating interactions with the bubble wall, a net chiral asymmetry will accumulate and bias the sphalerons to create a net baryon asymmetry. Some of this asymmetry is swept up by the advancing bubble wall as it expands, freezes in, and remains present to this day, generating the observed matter-antimatter asymmetry. This mechanism is known as electro-weak baryogenesis.

The most minimal model that can be investigated is obtained by extending the SM scalar sector by a real singlet scalar field. This addition allows for the possibility of a “strong” enough first-order electro-weak phase transition and hence the generation matter-anti-matter asymmetry at the electro-weak scale via electro-weak baryogenesis.

The model can be particularly challenging to observe since the singlet field has no direct couplings with the SM’s gauge or fermion sector. Indeed, a remnant scalar boson of the singlet field only attains its couplings to the SM particles via “mixing”, characterized by an angle θ. The result of this mixing is to endow a new scalar particle (h₂) with couplings identical to those of the Higgs boson, rescaled by the sine of θ. At the same time, the couplings of the SM-like Higgs boson (h₁) are reduced by the cosine of this angle, allowing for an indirect probe of this model through Higgs boson signal strength measurements at colliders. Furthermore, future colliders, including the high-luminosity LHC, present us with the unique opportunity to directly probe this model, by direct detection of a new scalar resonance. In particular, such a resonance should lie below ~1 TeV, if it has anything to do with electro-weak baryogenesis. Once such a scalar resonance is produced, it will primarily decay into pairs of gauge bosons (ZZ or WW) or pairs of SM-like Higgs bosons, provided that its mass is larger than twice the Higgs boson mass.

Our study, arXiv:2010.00597, demonstrated that a Future Circular Collider, colliding protons at 100 TeV, could very efficiently discover (or exclude), the existence of such a new scalar. It was shown that it would also be very likely that a 27 TeV upgrade to the LHC, i.e. a high-energy LHC, could also probe the parameter space thoroughly. Searches at these higher-energy proton colliders would be primarily driven by the gauge boson channels (h₂ to WW and ZZ), with substantial contributions coming from the Higgs boson pair channels (h₂ to h₁ h₁).

The upshot is that such colliders could exclude the prospect of generating the matter anti-matter asymmetry at the electro-weak scale. This would constitute a very significant clue in understanding its origin. On the other hand, taking a more positive point of view, future colliders could discover a new scalar particle that could be linked to a strong first-order phase transition. Our endeavours would then turn into verifying its origin and link to such a mechanism by solving the so-called “inverse problem”. In our recent study, arXiv:2108.11394, we performed first steps in this direction, with a “post-mortem’’ investigation that aims to address this issue by utilizing the first measurements that would follow the discovery of a new scalar boson. We demonstrated that at a 100 TeV proton collider, one could obtain precise measurements of the mass of the new boson, and through the combination of the h₂ → ZZ and h₂ → h₁ h₁ channels, one could obtain a combined fit for the strength of the triple interaction between an h₂ and two SM-like Higgs bosons (see figures below for an example).

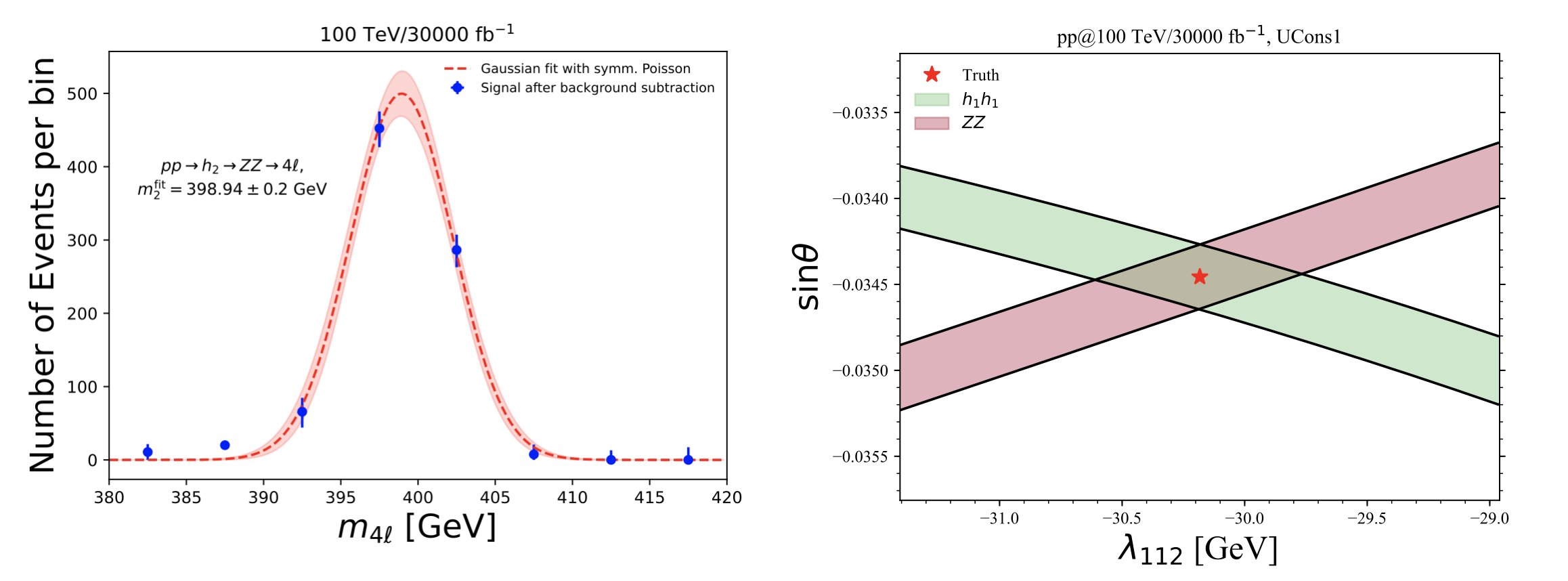
Figure 2: On the left we show an example of fitting the mass of the new scalar boson through the h₂ → ZZ → 4 leptons decay mode. On the right, we show, for a specific parameter space point, the uncertainty bands obtained by the cross section measurements of the pp → h₂ → h1 h1 and pp → h₂ → ZZ processes. Their overlap allows for a constraint on the triple scalar coupling between two SM-like Higgs bosons and the heavy scalar, h₂.

Despite the fact that precise measurements can be obtained, our study has demonstrated that these initial measurements would be insufficient to partition the parameter space in such a way that would allow us to associate a discovery with a strong first-order transition. Therefore, additional handles will be necessary. Luckily, there exist additional interesting processes that could act as such: multi-scalar processes like the asymmetric pp → h₁ h₂, or the symmetric pp → h₂ h₂, as well as Higgs boson triple production: pp → h₁ h₁ h₁. These would probe a combination of the parameters of the model through the scalar couplings, potentially allowing for further partitioning of the parameter space. We are currently investigating these processes in the context of strong first-order transition.

On top of additional collider information, there exists the exciting prospect of synergy between gravitational wave detectors and colliders. In fact, measuring gravitational waves, on top of qualitatively giving information on the nature of the electro-weak transition, by observing the peak frequency and peak amplitude, one could in principle fix two parameters in the real singlet-extended SM.

Finally, the question of the capabilities of future lepton colliders arises. The first stage of the FCC program (the FCC-ee) would potentially involve electron-positron collisions starting at the Z-pole (~91 GeV) and going up to 365 GeV. While the reach for direct production of a heavy scalar is constrained by the energy (see arXiv:1807.04284, Figure 2 for cross sections of the dominant processes), this lepton collider can achieve an unprecedented precision in electro-weak observables that may indirectly probe models of electro-weak baryogenesis. In particular, running at 250 GeV, it was shown in arXiv:1709.06103, that the sine of the mixing angle could be constrained down to ~0.052. In addition, arXiv:1608.06619 considered the constraints on the Higgs-Z-Z coupling directly for various lepton colliders. Finally, constraints on the triple Higgs boson coupling, of up to 40% could be obtained (arXiv:1711.03978), imposing an additional constraint on models containing a real singlet field. Future studies should further asses prospects of the FCC-ee in addressing electro-weak baryogenesis, e.g. through indirect effects containing heavy scalars in loops or even by considering direct production of lower-mass scalars in more challenging models of extended scalar sectors.

Whatever the true mechanism of baryogenesis is in Nature, one thing is certain: the LHC and future lepton or proton colliders will have something to tell us about this question, either by discovery or exclusion of its manifestation at the electro-weak scale.