When I started my career as a theoretical physicist in the early 1980’s, the Higgs boson was not yet a topic of major theoretical interest.  There was a long gap between the time when the Brout- Englert-Higgs mechanism was proposed and when people really started doing some hard calculations.   Following the seminal 1976 paper of Ellis, Gaillard, and Nanopoulos with the now infamous quote,

“We should perhaps finish with an apology and a caution.  We apologize to experimentalists for having no idea what is the mass of the Higgs boson, unlike the case with charm and for not being sure of its couplings to other particles, except that they are probably all very small.  For these reasons we do not want to encourage big experimental searches for the Higgs boson, but we do feel that people performing experiments vulnerable to the Higgs boson should know how it may turn up.”

there was a general understanding that the Higgs boson could be found anywhere (π and K decays, B decays, who knows?) and that it would be necessary to search for the Higgs boson in many different types of experiments. Since the mass of the Higgs boson is a free parameter in the theory, theorists began to do simple studies of how the Higgs could be observed with various  assumptions about the Higgs mass.

The 1977 paper of Lee, Quigg and Thacker had a major impact on the physics community’s understanding of how to look for the Higgs boson. The thinking at the time was that because of possible unitarity violations in the high energy scattering of gauge bosons, either the Higgs boson was lighter than around 800 GeV or there would be some new physics at the few TeV scale beyond that predicted at the Standard Model resulting from the violation of perturbative unitarity. This led to the so-called no-lose theorem: “The LHC and the SSC had to find something”. If the Higgs boson weren’t found, the thinking went, then there would be supersymmetry, technicolor, or something new at the energy scales accessible to the LHC and SSC that would restore perturbative unitarity. It is impossible to over emphasize the impact of this reasoning as it triggered serious thinking about how the Higgs boson could be observed at  a hadron collider. This logic led to a flood of interesting and important model building centered around finding the Standard Model Higgs boson, and to the study of the experimental consequences of extensions of the theory.

My first post-doctoral position was at Fermilab, where discussions of the Higgs boson and how to discover it were frequent. The LEP collider was under construction, and theorists were hoping that the Higgs boson would be discovered there. The lore at the time was that it was extremely difficult to find new and unexpected physics of any type at a hadron machine. The first systematic exploration of the possibilities for finding the Higgs boson at a hadron machine was the 1984 paper of Eichten, Hinchliffe, Lane, and Quigg which consisted of calculating total cross sections and basic distributions for various processes, including the Higgs boson. Inspired by this work, I began to think seriously of how the Higgs boson could be seen at high energy hadron colliders. You had to know what you were looking for, because there are so many events at the LHC that have nothing to do with the Higgs boson. Otherwise, it would be like looking for a needle in a haystack. The Higgs was discovered, for example, by its decay to two photons and there are millions of two-photon events at the LHC that have nothing to do with the Higgs. Theory told us how to look for the Higgs boson, and I think it was really important that a trail was set out to follow. This involves calculating how often you make a Higgs boson and what the background might look like.

I decided to calculate the first order QCD corrections to the production of a Higgs boson from gluon- gluon scattering in the limit of an infinitely heavy top quark mass. Shifman and other Russians had derived low energy theorems demonstrating that the interactions between the Higgs boson and gluons  simplified in the heavy top quark limit.  (Reading the Russian papers at the time was an adventure involving searching for exactly the right orange preprint, or if you were lucky, the journal article in the far reaches of the physics library). Today, graduate students are given the calculation of the leading QCD corrections to Higgs production from gluons as a homework problem, but for me at the time it was a difficult project. The tools for algebraic evaluation of Feynman rules were primitive and much of the calculation was done by hand.

At the same time as I was performing this calculation, Djouadi, Spira, and Zerwas were doing the same calculation (but without the assumption of an infinitely heavy top quark mass). The results were surprising to us when we found that the rate for Higgs production was more than doubled when the QCD corrections were included. This was the beginning of the realization that higher order QCD corrections could impact searches for the Higgs boson and were crucial for predicting rates. Now, of course, we know most Higgs cross sections to NNLO in QCD and NLO in the electroweak interactions.  The   program of computing higher order corrections to Higgs processes has required both creative new mathematical methods and new computer algorithmic techniques for the calculations. The theoretical evaluation of the Higgs rate from gluon fusion has proceeded at a steady rate from the early NLO calculations to a stage where we not only have the N3LO calculations, but we also have the inclusion of many higher order logarithms with the result agreeing very well with the experiment. The plot below shows how with each theoretical improvement, the prediction gets closer to the experimental result and the theoretical uncertainties become smaller.

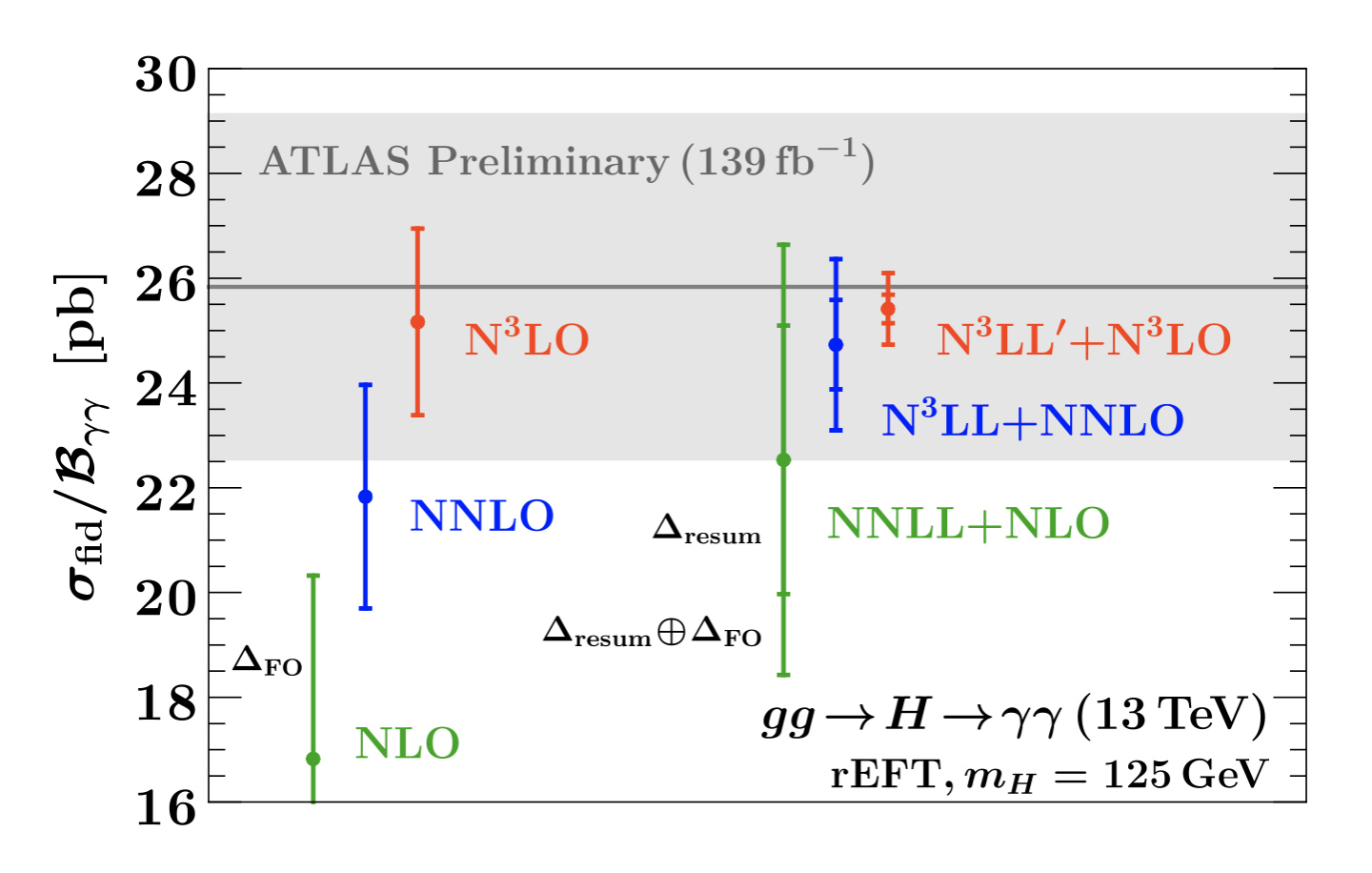
Figure from arXiv: 2102.08039

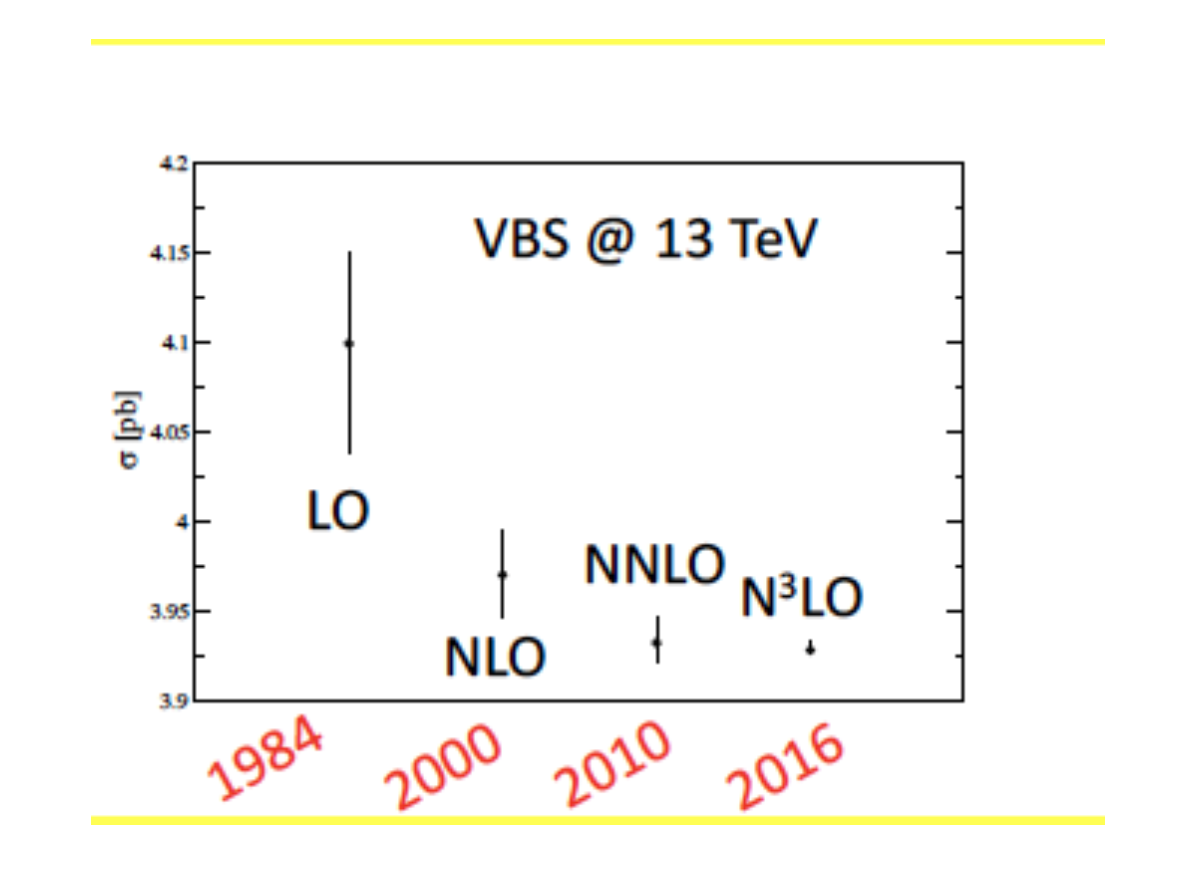
A second major theoretical advancement in the study of the Higgs boson in the 1980’s was the exploration of production mechanisms other than gluon fusion. Theorists quickly realized that the W and Z could be considered as partons in the proton leading to logarithmically enhanced rates at high energy for the WW fusion into a Higgs boson. Dieter Zeppenfeld and his collaborators systematically included WW fusion into the computer code VBFNLO and began a long program of implementing higher order QCD corrections in a way that could be used by the experimentalists. By now, sophisticated calculations include vector boson fusion to NNLO QCD as seen in the figure below. As with gluon fusion, we see the progression in time of ever smaller error bars in the theoretical predictions and observe that it has taken 30 years to get to our current understanding, with a long time gap between the LO and the NLO results.

By the end of the 1980’s, theorists had a reasonable grasp on the expected Higgs boson properties, so with Haber, Gunion and Kane, I decided to write down everything I knew about the Higgs boson in the Higgs Hunter’s Guide.  Much of this book is out-dated now (E6 models anyone?), but the discussion of  extended Higgs sectors remains extremely relevant as the current and future experimental searches push our knowledge of the Higgs sector with ever more precise measurements and increasingly sensitive searches for new Higgs-like particles. A new version of the Higgs Hunter’s Guide would be many times longer than the original!

The steadily increasing precision in the calculations of Higgs production and decay enables the LHC to truly be a machine for precision Higgs physics. It is particularly interesting to see the interplay of theory and experiment. With the HL-LHC, the experimental precision on Higgs couplings will be greatly increased from the current measurements, requiring that theorists decrease the uncertainties on the predictions. 

Currently, the interpretation of HL-LHC Higgs measurements is expected to be limited by theory, inspiring theorists to tackle increasingly difficult calculations. This back and forth between theory and experiment is critical for future discoveries in the Higgs sector!

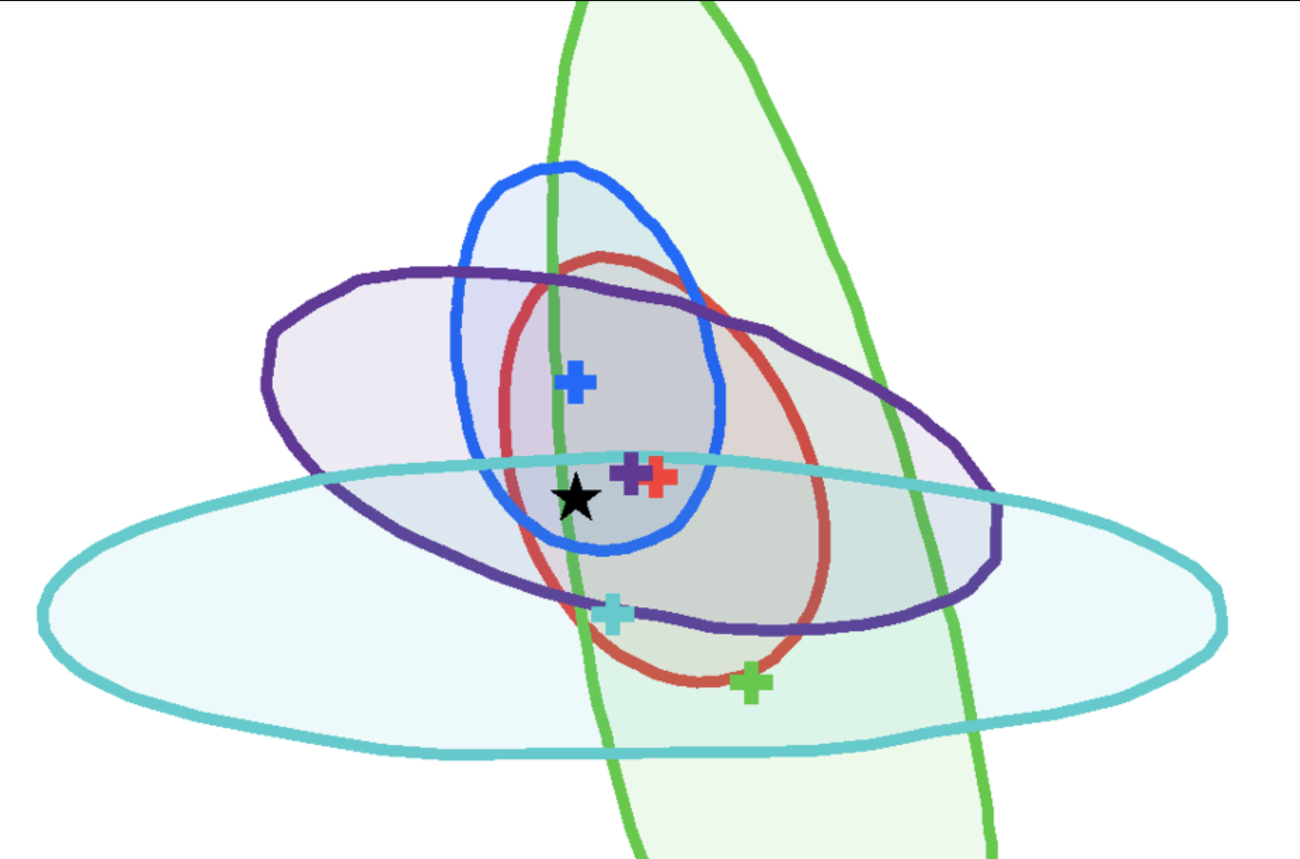
Note from the editor: Top image shows likelihood contours in the plane of two types of coupling (those which involve a W or Z boson on the vertical axis, and those which don’t on the horizontal) from a fit to the combination of ATLAS and CMS data, shown for the five decay channels, H→ ZZ, H→ WW, H→γγ, H→ττ, and H→ bb. The results are shown as 68% CL contours, together with the best-fit values to the data, and the Standard Model expectation. Credits: ATLAS and CMS/CERN