The observation of electroweak symmetry breaking in nature implies the existence of Goldstone bosons that provide the longitudinal components of the massive W and Z gauge bosons. A priori, one could have imagined a plethora of possible dynamical models that produce the required Goldstone bosons. Remarkably, the simplest possible model, a self interacting complex doublet of elementary scalar fields, which yields a physical scalar particle—the Higgs boson, is consistent with all current experimental data. Nevertheless, a number of profound theoretical questions remain which suggest that the complete story of electroweak symmetry breaking has not yet been written. In the paragraphs below, I will briefly discuss the current status of Higgs boson physics and explore some of the implications for future Higgs studies (following the lecture originally presented in Ref. [1]).

On July 4, 2012, the discovery of an electrically neutral scalar particle with a mass of about 125 GeV at the Large Hadron Collider (LHC) was announced. After ten years of data collection and analysis, it has been determined that the properties of this scalar particle closely resemble those of the Higgs boson that was predicted by the Standard Model (SM) of particle physics. At the LHC, Higgs bosons are produced by a variety of mechanisms, the most important of which is gluon-gluon fusion (ggF). Once produced, the Higgs boson can decay into a variety of final states. The relevant experimental observable is the product of the cross section (σ) of a given production mechanism multiplied by the branching ratio (B) for Higgs boson decay into the observed final state. In Fig. 1, the product σB for the various production mechanisms and final state decay products, observed by the ATLAS Collaboration [2], is compared with the corresponding SM predictions. A similar plot obtained by the CMS Collaboration can be found in Ref. [3].

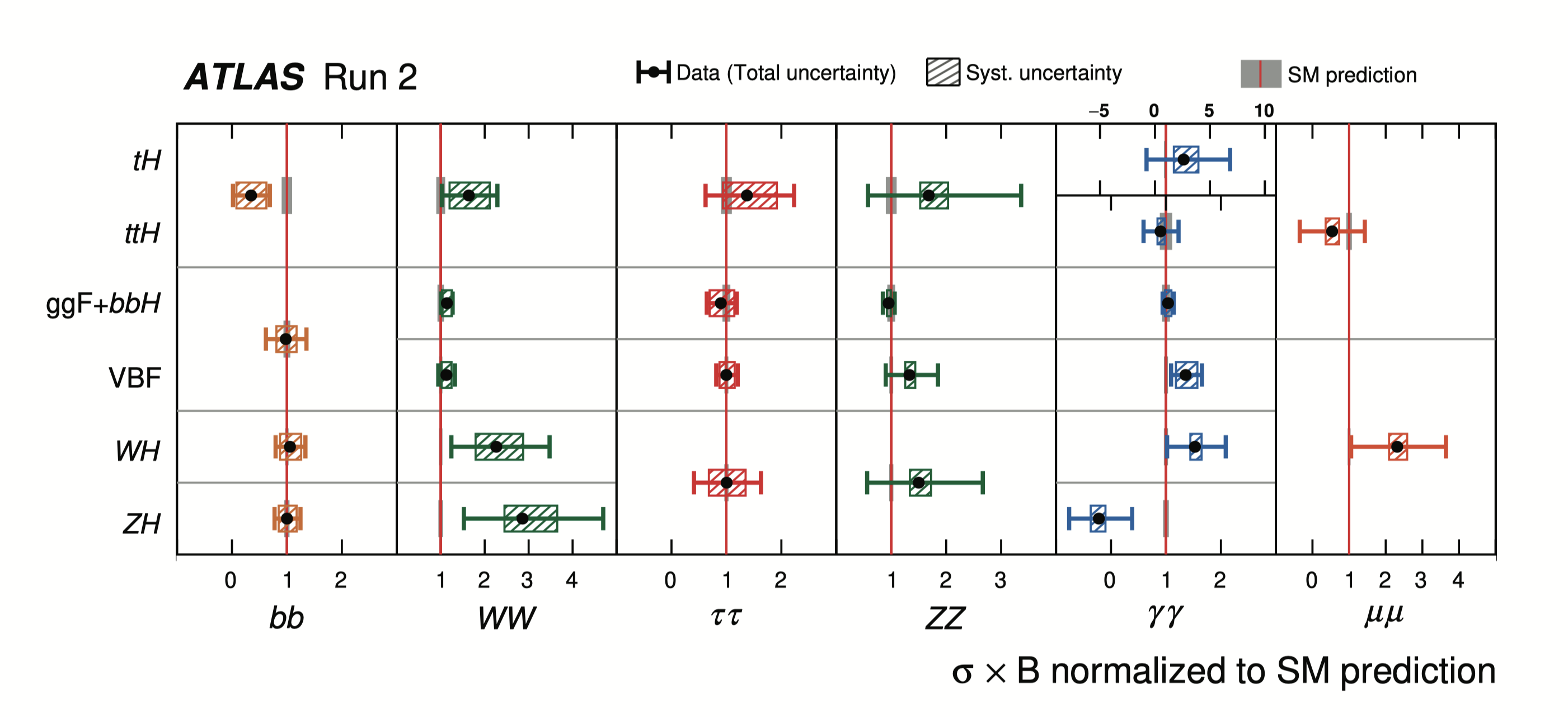
Figure 1: Ratio of observed rate to predicted SM event rate for different combinations of Higgs boson production and decay processes, as observed by the ATLAS Collaboration. The horizontal bar on each point denotes the 68% confidence interval. The narrow grey bands indicate the theory uncertainties in the SM cross section times the branching fraction predictions. The p-value for compatibility of the measurement and the SM prediction is 72%. Taken from Ref. [2].

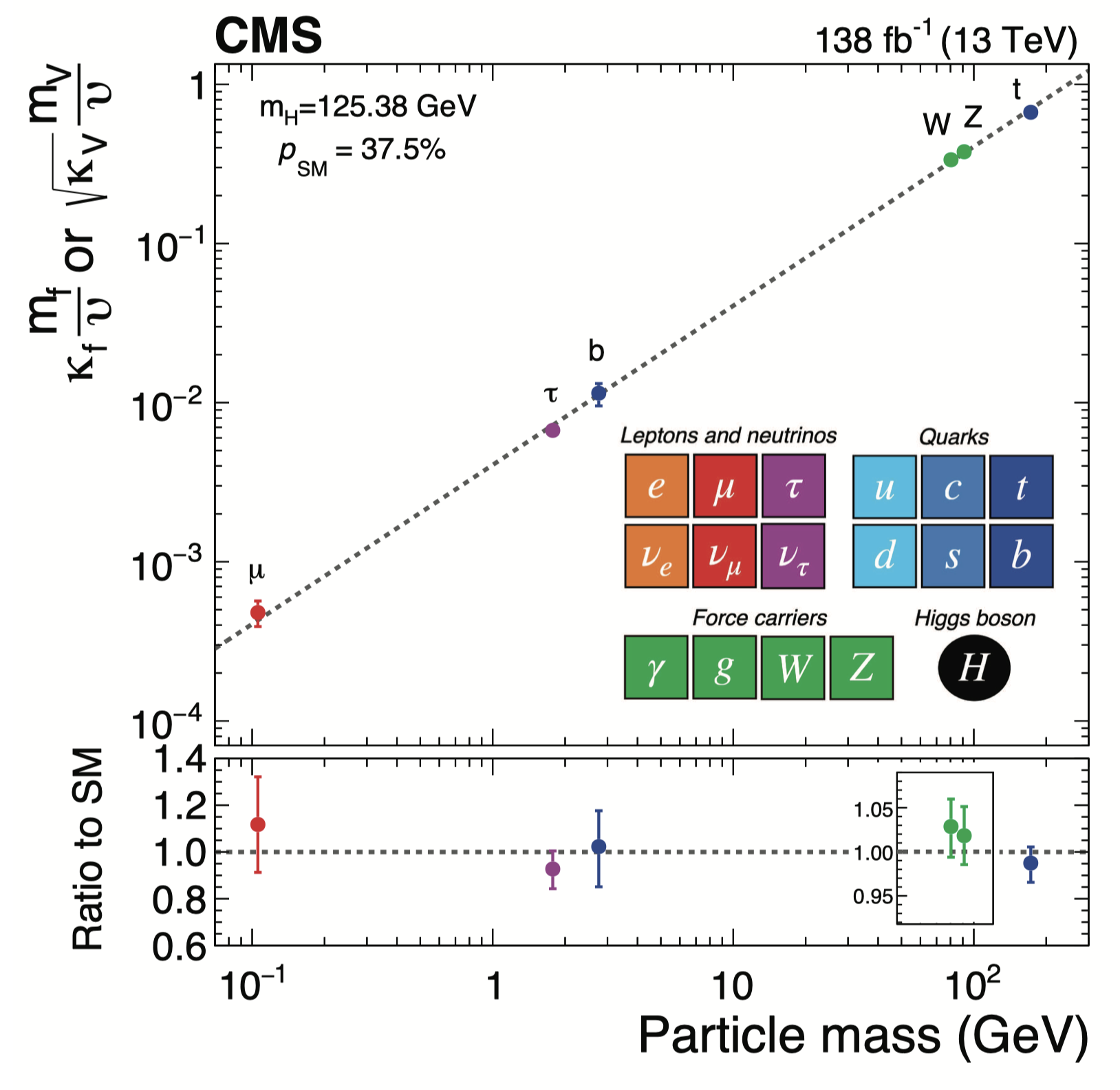
Figure 2: The measured coupling modifiers of the Higgs boson to fermions and heavy gauge bosons, observed by the CMS Collaboration, as functions of fermion or gauge boson mass, where v is the vacuum expectation value of the Higgs field. For gauge bosons, the square root of the coupling modifier is plotted, to keep a linear proportionality to the mass, as predicted in the SM. The p-value with respect to the SM prediction is 37.5%. Taken from Ref. [3].

The Higgs boson is intimately connected with the mechanism of mass generation for the fundamental particles (quarks, charged leptons and gauge bosons) of the SM. As a result, the SM Higgs boson couples to fermions [gauge bosons] with a strength that is proportional to the corresponding fermion mass [gauge boson squared mass]. This expected behavior is experimentally reproduced in Fig. 2 based on results obtained by the CMS Collaboration [3]. A similar plot obtained by the ATLAS Collaboration can be found in Ref. [2]. The results shown in Figs. 1 and 2 provide a quantitative measure of the consistency of the Higgs boson properties with those predicted by the SM.

Although the SM has been remarkably successful in describing the behavior of the fundamental particles and their interactions, the SM cannot be the ultimate theory of the fundamental particles and their interactions. Putting aside a few experimental anomalies that could be statistical flukes or could be evidence of cracks in the SM, there exist a number of important clues that strongly suggest the need for new physical laws beyond the Standard Model (BSM). For example, the astrophysical evidence for dark matter cannot be explained in the context of the SM, and may be a consequence of a new particle associated with BSM physics. Another hint for BSM physics arises when attempting to devise a theory of baryogenesis in the early universe to explain the observed asymmetry between baryons and their antiparticles, which cannot be explained by SM physics alone. Finally, the origin of the energy scale of electroweak symmetry breaking remains a mystery. (Theorists regard the Higgs sector of the SM as unnatural; for more details, see Ref. [4].) This observation has motivated many attempts to introduce BSM physics that might be revealed in experimental studies at the LHC (although so far no definitive evidence for BSM phenomena has yet to be detected).

One notable feature of the SM is the minimal structure of the scalar sector of the theory. In light of the nonminimality of the fermion and gauge sectors, it is tempting to suggest that the scalar sector of the theory should be nonminimal as well. Indeed, there are numerous motivations for considering an extended Higgs sector. For example, extended Higgs sectors can provide a dark matter candidate and can modify the electroweak phase transition in a way that facilitates baryogenesis in the early universe. In addition, the consistency of some models of BSM physics requires the introduction of additional scalar states beyond the SM Higgs boson.

One cannot arbitrarily extend the Higgs sector of the SM due to a number of important constraints arising from observed experimental data. For example, the electroweak ρ parameter, which is measured to be very close to 1, significantly restricts the possible scalar multiplets (while allowing for electroweak doublets of hypercharge one and electroweak singlets). The experimental rarity of flavor-changing neutral currents imposes significant restrictions on the structure of the Higgs couplings to fermion pairs. Finally, given that the Higgs boson so far appears to be SM-like, any model that extends the Higgs sector beyond the SM must contain one scalar state that can be identified with the SM-like Higgs boson observed at the LHC.

The last two phenomenological constraints are satisfied in certain limiting cases of extended Higgs models, called the flavor alignment limit and the Higgs alignment limit, respectively. Flavor alignment posits that all Higgs-fermion Yukawa matrices are aligned with the corresponding fermion mass matrices (which eliminates flavor changing neutral currents mediated by neutral scalar exchange in the Higgs Lagrangian). Higgs alignment posits that in a scalar field basis where only one of the Higgs doublet fields possesses a nonzero vacuum expectation value, the associated neutral scalar field that resides in the same doublet is an approximate mass eigenstate field (to be identified with the SM-like Higgs boson observed at the LHC).

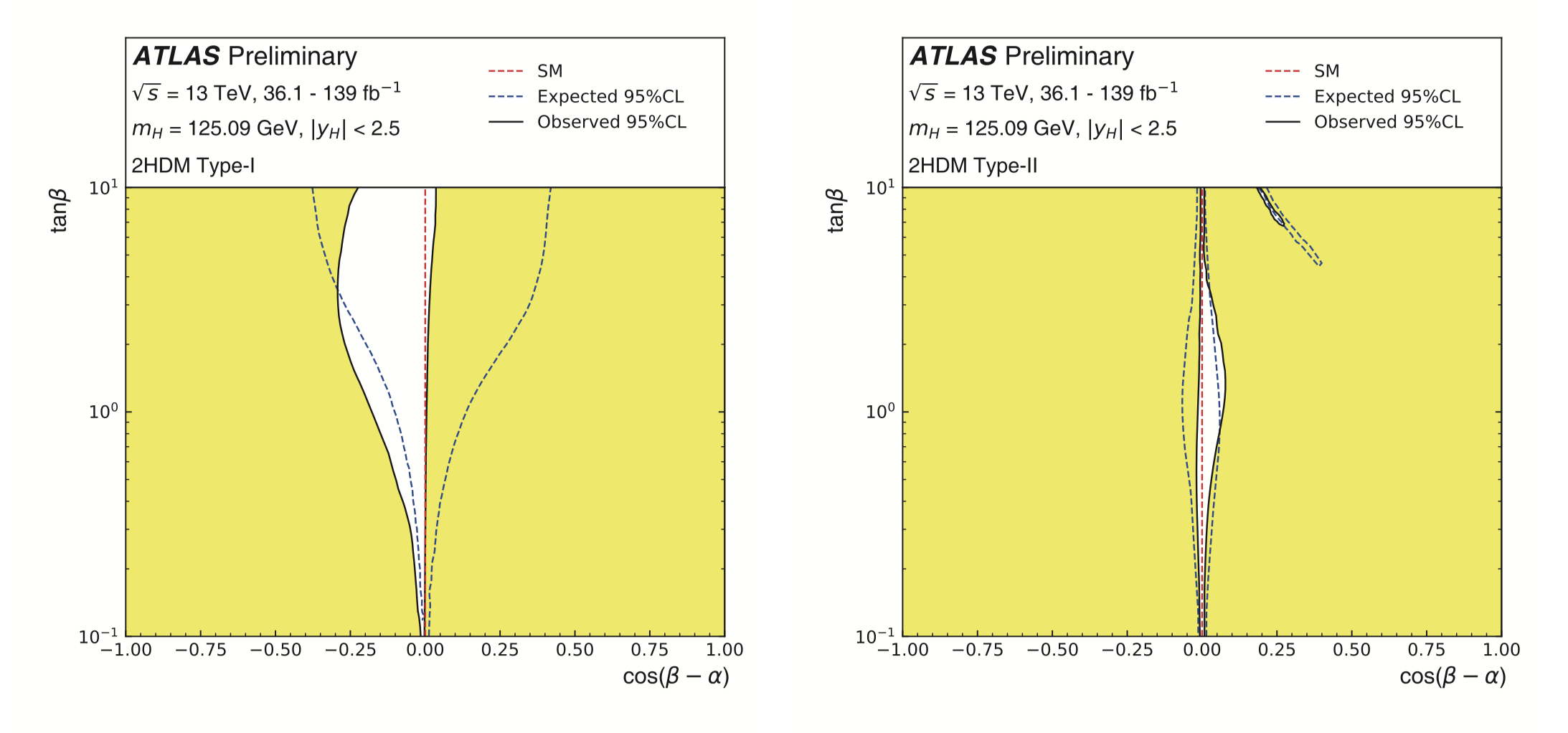
Figure 3: Regions excluded (at 95% CL) by fits to the measured rates of the productions and decay of the Higgs boson (assumed to be h of the 2HDM), highlighted in yellow. The observed best fit values for cos(β − α) are −0.006 for the Type-I 2HDM and 0.002 for the Type-II 2HDM. Taken from Ref. [7].

To illustrate these two constraints, consider the two Higgs doublet model (2HDM), in which a second Higgs doublet is added to the SM [5]. One can introduce a symmetry that enforces flavor alignment, which leads to the so-called Type I and Type II 2HDMs. If CP conservation is imposed on the scalar potential, then the departure from the Higgs alignment limit is characterized by one parameter called cos(β-α) in the literature [which is zero if the Higgs alignment limit were exact]. In the CP-conserving 2HDM near the alignment limit, cos(β−α) ≃ Z₆v²/(m_h² −m_H²), where h is the SM-like Higgs boson, H is a heavier neutral CP-even scalar of the 2HDM, v ≃ 246 GeV is the Higgs field vacuum expectation value, and Z₆ is a parameter that depends on the 2HDM scalar potential [6]. Thus, the Higgs alignment limit is approximately realized if either m_H ≫ m_h (called the decoupling limit) or if |Z₆| ≪ 1. In Fig. 3, regions of the 2HDM parameter space highlighted in yellow are excluded by the current precision of the LHC Higgs data by the ATLAS Collaboration [7], which implies that the parameters of the 2HDM must respect an approximate Higgs alignment limit in order to be consistent with current LHC observations.

In July, 2022, Run 3 of the LHC commenced, with an expectation of doubling the presently available Higgs boson data sets. In addition to improving the precision of the measurements of the previously observed Higgs boson, the ATLAS and CMS Collaborations will continue their searches for additional scalar states that could populate an extended Higgs sector. Anticipating the results of Run 3 as well results that might emerge from the High Luminosity phase of LHC (which will begin at the end of this decade) as well as potential results from future collider facilities presently under development, I have assembled the following two Higgs wishlists. One wishlist focuses on the SM-like Higgs boson h, while the second wishlist concerns new scalar states beyond the SM.

Concerning h, whose experimental profile is well established after ten years of LHC data:

1. What are the coupling strengths of h to second generation quarks (c, s)?

2. Will we ever be able to determine the coupling strengths of h to first generation quarks (u, d) and/or gluons?

3. What will it take to measure the coupling strength of h to electrons?

4. Will sufficient precision ever exist to measure the invisible decay partial width expected in the SM (h → ZZ^∗ → νννν)? How well can we constrain the branching ratio of h into invisible final states (that might be present in certain BSM scenarios).

5. With what ultimate accuracy can one predict the properties (cross sections, partial widths, etc.) of the SM Higgs boson? What are the important missing theoretical computations that need to be done?

6. How well can one determine the Higgs self-coupling? To what extent (and with what accuracy) can one experimentally reconstruct the Higgs scalar potential?

7. With what accuracy and reliability can one experimentally determine the total decay width of h?

8. Will experimental deviations from SM Higgs boson properties, if observed, be convincing? Will they reveal a new energy threshold for BSM physics?

9. Do Higgs bosons couple to a dark sector made up of new particles that are completely neutral with respect to the SM (the so-called “Higgs portal”)?

10. Will convincing data emerge that implies that h is not an elementary scalar but is in fact a composite state of more fundamental entities?

Concerning Higgs physics beyond the SM:

1. How many generations of Higgs scalars exist at or below the TeV scale and what are their electroweak quantum numbers?

2. Are there any new elementary scalars not yet discovered with masses below the mass of the SM-like Higgs boson? For example, do axion-like particles exist?

3. How small is the departure from the Higgs alignment limit, and what is the underlying mechanism that yields an approximate Higgs alignment?

4. Does the unitarization of the scattering of longitudinal gauge bosons require additional scalars from an extended scalar sector?

5. How does the extended scalar sector affect the electroweak phase transition? Does it permit electroweak baryogenesis? Does it play other significant roles in early universe cosmology (e.g., inflation)? Will future gravitational wave experiments shed any light on these matters?

6. How small is the departure from the flavor alignment limit of the neutral Higgs–fermion Yukawa couplings? Will quark/lepton flavor off-diagonal couplings of neutral scalars be observed?

7. Are there new sources of CP violation associated with the extended scalar sector? Can these be experimentally observed (and can the corresponding sources be identified)?

8. Do neutral scalars comprise a significant fraction of the dark matter?

9. Beyond the scalar sector, can one identify any associated BSM phenomena? How does the scalar sector inform the identification of the BSM physics? Will this shine any light on the apparent unnatural nature of the SM Higgs sector?

10. Will the extended Higgs sector reveal evidence for substructure in the scalar sector?

In 1990, The Higgs Hunter’s Guide [8] summarized the theory and provided a roadmap for searching for the Higgs boson of the SM and additional scalar states of an extended Higgs sector at high energy collider facilities. The discovery of the Higgs boson h at the LHC in 2012 and the analysis of its properties in the Run 1 and Run 2 LHC Higgs data sets over the past ten years strongly suggest that h is either the Higgs boson of the SM or a very close facsimile. Nevertheless, there is still room for surprises. Evidence for additional scalar states (which would arise in models of extended Higgs sectors) and/or other BSM phenomena could emerge in future runs at the LHC or at new collider facilities that might be constructed in the future. Indeed, by considering the questions posed in the Higgs wishlists above, one can compare and contrast the strengths and weaknesses of various proposed future collider facilities in addressing the key questions of Higgs physics.

Note: This writeup is a condensed version of a talk of the same title originally presented at the 49th SLAC Summer Institute (SSI 2021) on August 27, 2021 (see Ref. [1]).

References

[1] H.E. Haber, “Higgs Boson Physics—The View Ahead,” summary talk of the 2021 SLAC Summer Institute (SSI 2021): The Higgs State Fair. The slides and video of the talk are available at https://indico.slac.stanford.edu/event/6758/contributions/2648/.

[2] The ATLAS Collaboration, “A detailed map of Higgs boson interactions by the ATLAS experiment ten years after the discovery,” Nature 607, no. 7917, 52-59 (2022) [arXiv:2207.00092 [hep-ex]].

[3] The CMS Collaboration, “A portrait of the Higgs boson by the CMS experiment ten years after the discovery,” Nature 607, no. 7917, 60-68 (2022) [arXiv:2207.00043 [hep-ex]].

[4] N. Craig, “Naturalness: A Snowmass White Paper,” [arXiv:2205.05708 [hep-ph]].

[5] G.C. Branco, P.M. Ferreira, L. Lavoura, M. N. Rebelo, M. Sher and J.P. Silva, “Theory and phenomenology of two-Higgs-doublet models,” Phys. Rept. 516, 1-102 (2012) [arXiv:1106.0034 [hep-ph]].

[6] D.M. Asner, T. Barklow, C. Calancha, K. Fujii, N. Graf, H.E. Haber, A. Ishikawa, S. Kanemura, et al. “ILC Higgs White Paper,” [arXiv:1310.0763 [hep-ph]].

[7] The ATLAS Collaboration, “Combined measurements of Higgs boson production and decay using up to 139 fb⁻¹ of proton-proton collision data at √ s = 13 TeV collected with the ATLAS experiment,” ATLAS-CONF-2021-053 (December 15, 2021).

[8] J.F. Gunion, H.E. Haber, G.L. Kane and S. Dawson, The Higgs Hunter’s Guide (Westview Press, Boulder, CO, 2000).