In 1928, a young Paul Dirac wrote one of the most spectacular papers of modern physics when he successfully unified two distinct theories, quantum mechanics and special relativity. What arose from his equations was a prediction of a new form of matter, antimatter, which was discovered just four years later by Carl Anderson through the first observation of a positron passing through the Earth’s atmosphere. Matter and antimatter are not independent entities and transitions between them are allowed by quantum theory. This was first proposed by Murray Gell-Mann and Abraham Pais in 1955, in order to describe the properties of θ⁰ and θ⁰ particles, now called K⁰ and K⁰. By considering the K⁰ and K⁰ system as a two-state system, Gell-Mann and Pais provided the first theoretical description of neutral meson mixing, a phenomenon later observed experimentally in 1960 at Berkeley. Later, in 1964, studying decays of neutral kaons, James Cronin and Val Fitch made the significant discovery that charge-parity (CP) symmetry, that which relates matter to antimatter, is violated. CP violation is a key ingredient in the quest to understand the observed matter-antimatter asymmetry of the Universe: we see approximately one baryon for every photon but almost no anti-baryons at all.

In order to incorporate CP violation into the Standard Model (SM) of Particle Physics, Makoto Kobayashi and Toshihide Maskawa realised that a third generation of quarks was required, and predicted the existence of the top and beauty quarks. Based on the work of Nicola Cabibbo, they introduced the Cabibbo-Kobayashi-Maskawa (CKM) quark mixing matrix, which describes the relative strengths of the charged current processes of the weak interaction, mediated by the W bosons, allowing quarks to change flavour. More recently, CP violation has been observed in both the beauty and charm sectors, as predicted by the CKM mechanism.

The CKM matrix is unitary in the Standard Model; a mathematical condition that can be expressed as a triangle, such as the one shown in Figure 1. For a detailed review please see the PDG article available here. Two of the triangles vertices are fixed, at (0,0) and (1,0), with the other remaining free, and the area of the triangle is proportional to the total amount of CP violation in the quark sector. Therefore there are just two free parameters of this triangle if the unitary condition is maintained. However, experimentally we have five different parameters that can be measured - the three internal angles and the length of two sides - which allows us to over-constrain the triangle and determine whether unitarity is upheld. If it is not, this would be a clear sign of New Physics contributing to CP violation in the quark sector. The angles θ, β and γ are CP-violating phases that effectively allow for different decay rates for a given particle and antiparticle transition.

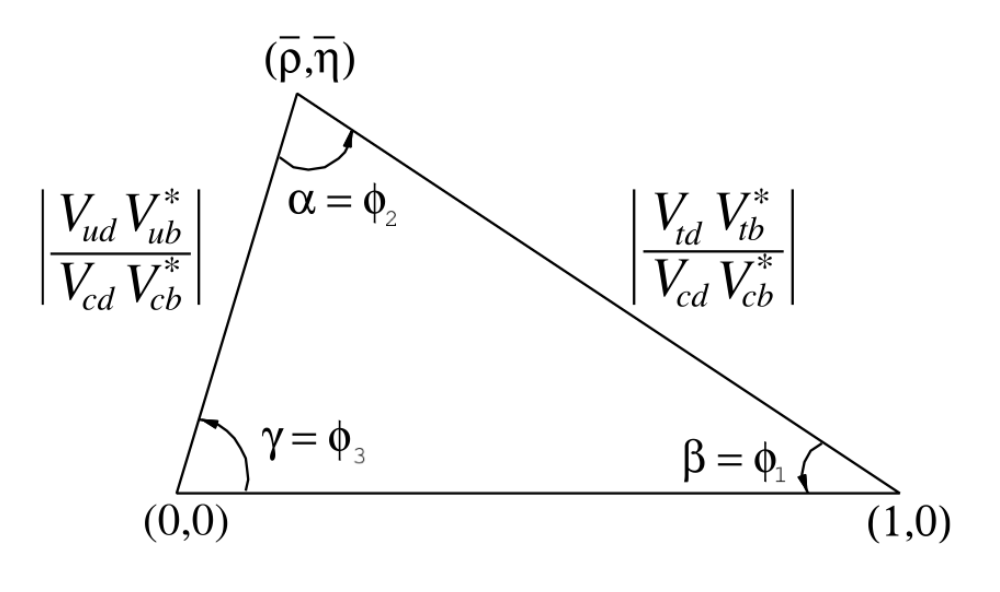
Figure 1: The unitarity triangle. The V_ij terms are complex CKM elements describing the coupling strength between quarks i and j. Figure reproduced from the PDG report here

The CP-violating angle γ of the CKM matrix is a standard candle of the Standard Model, since it can be determined in an entirely data-driven way with negligible theoretical uncertainty. Comparisons between direct and indirect measurements of γ provide a powerful test for New Physics. Before LHCb began taking data, γ was one of the poorest known constraints of the CKM unitarity triangle, but that is no longer the case.

Measurements of the angle γ are performed by studying B meson decays that proceed via two paths; a → bc quark level transition and a → bu quark level transition. Figure 2 shows example Feynman diagrams for these processes in B^- → DK^- decays. An interference occurs when the D⁰ and D⁰ mesons decay to the same final state. The angle can then be determined by comparing the decay rates of the B⁺ measurement and its antimatter partner, the B^-. See this recent LHCb paper for more details.

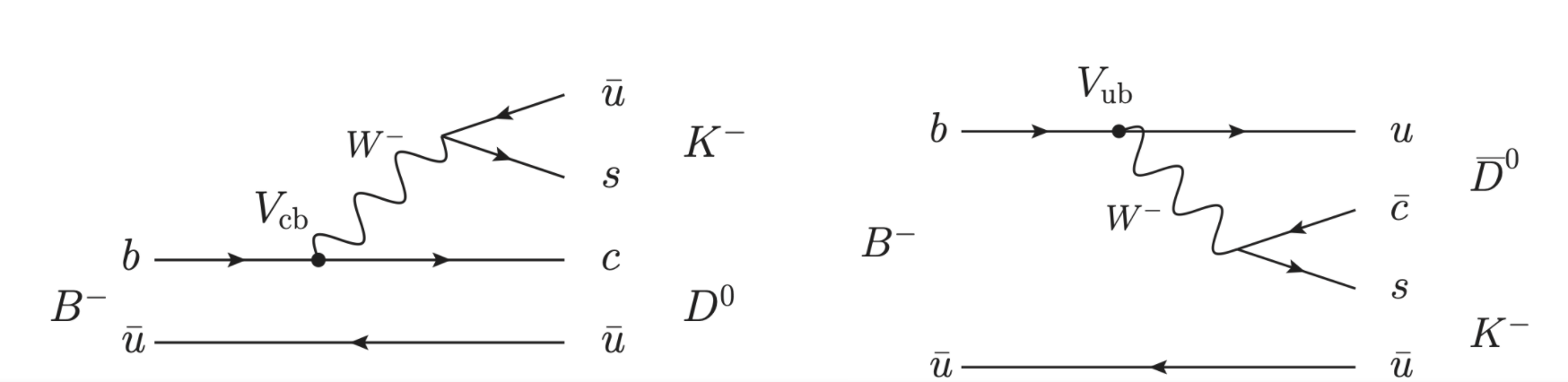
Figure 2: Feynman diagrams for B^-DK^- decays that are used to measure the angle when the D⁰ and D⁰ mesons decay to the same final state.

LHCb’s latest result marks an important change in strategy, by including not only results from beauty decays sensitive to γ but additionally exploiting the sensitivity to CP violation and mixing in charm meson (D⁰) decays. Mixing in the D⁰ - D⁰ system proceeds via flavour-changing neutral currents, which may be affected by contributions from new heavy particles, and is described by two mixing parameters; the mass, x, and width, y, difference between the two charm flavour states. The parameter x is connected to the oscillation period of a D⁰ to a D⁰ meson and is measured to be very small, with an oscillation rate over one hundred times longer than the average lifetime of a D⁰ meson. Theoretical predictions of x and y are challenging to perform, so experimental determinations provide powerful constraints for alternative predictions of the charm sector.

The new combination uses over twenty LHCb beauty and charm measurements and determines γ=(65.4^+3.8_-4.2 )°(see Figure 3, right), the most precise measurement from a single experiment. Furthermore, charm mixing parameters are determined by combining, for the first time, both the beauty and charm datasets, which gives x = (0.400^+0.052_-0.053)% and y = (0.630^+0.033_-0.030)%(see Figure 3 left). The latter is a factor of two more precise than the current world average, which is entirely due to the new methodology that harnesses additional sensitivity to the charm sector from the beauty decays used to measure γ.

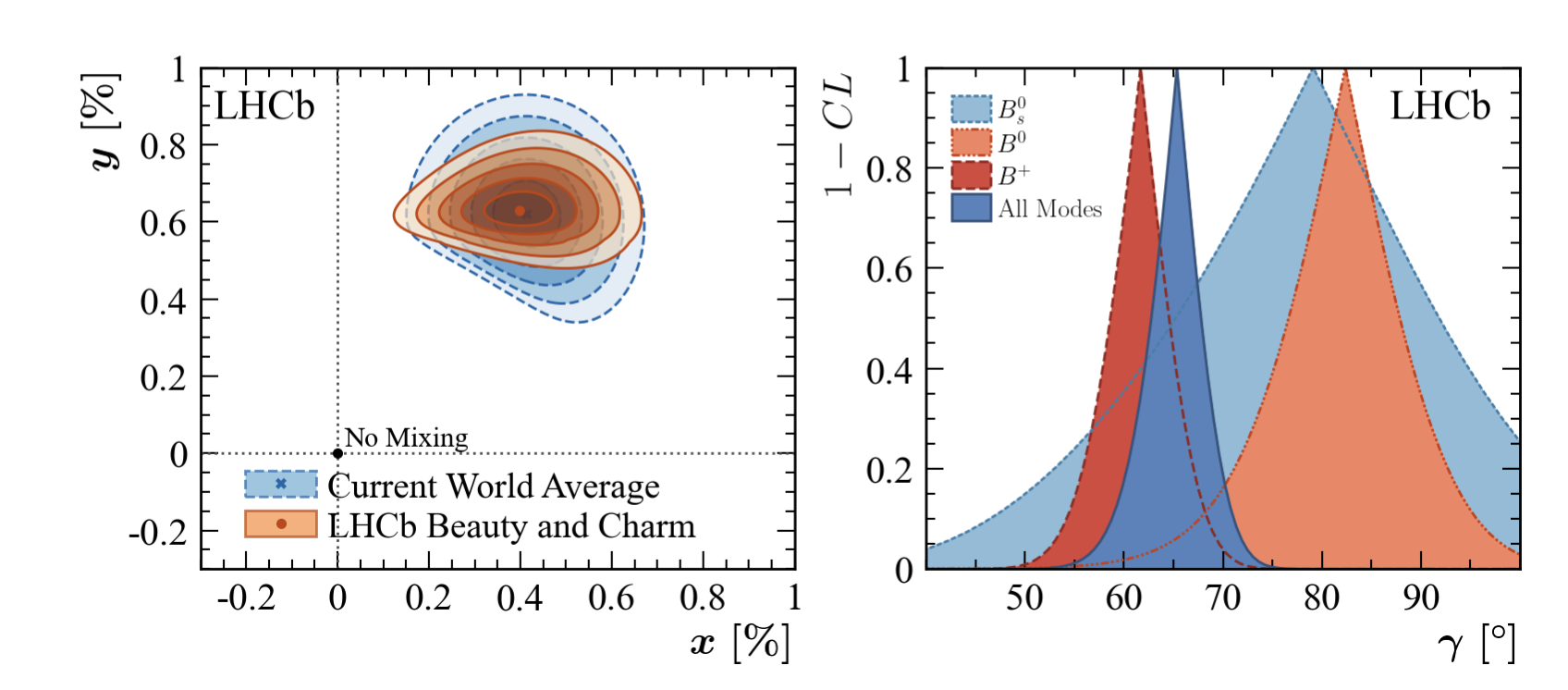
Figure 3: Left: New (orange) constraints for the charm mixing parameters x and y compared to the current world average (blue). Contours are drawn from 1-5 standard deviations. Right: A comparison of the sensitivity to CKM angle γ with all beauty and charm modes (dark blue, solid line) and those just originating from B_s⁰ (light blue, dotted line), B⁰ (orange, dash-dotted line) and B⁺ (red, dashed line) initial states. 

In a new paper, LHCb analysed the decays of D⁰ mesons into K^–K⁺, π^–π⁺ and K^–π⁺ meson pairs. LHCb is an ideal charm factory, where the precision of its subdetectors allows large samples of two-body charm decays to be reconstructed with high purity, as can be seen in Figure 4. 

Figure 4: The three images show the size and purity of the D⁰ → K^-π⁺, D⁰ → K^-K⁺ and D⁰ → π^-π⁺ decay samples, where almost one hundred million D⁰ mesons are recorded with low levels of background.

Due to the D⁰ - D⁰ mixing, the measured lifetime of a D⁰ → K^-π⁺ decay slightly differs to that measured from a D⁰ → K^-K or a D⁰ → π^-π⁺ decay. The difference is measured via the quantity y_CP^f – y_CP^Kπ , which is closely related to the parameter y. A measurement of this quantity can therefore improve our experimental knowledge of charm mixing.

Using a precise reconstruction strategy of the D⁰ mesons decays, the ratios R^f(t) of the number of D⁰→f decays over D⁰K^-π⁺ decays as a function of the measured D⁰ decay time t are built. The measured slope of R^f(t) gives the values of y_CP^KK – y_CP^Kπ and y_CP^ππ – y_CP^Kπ as shown in Figure 5.

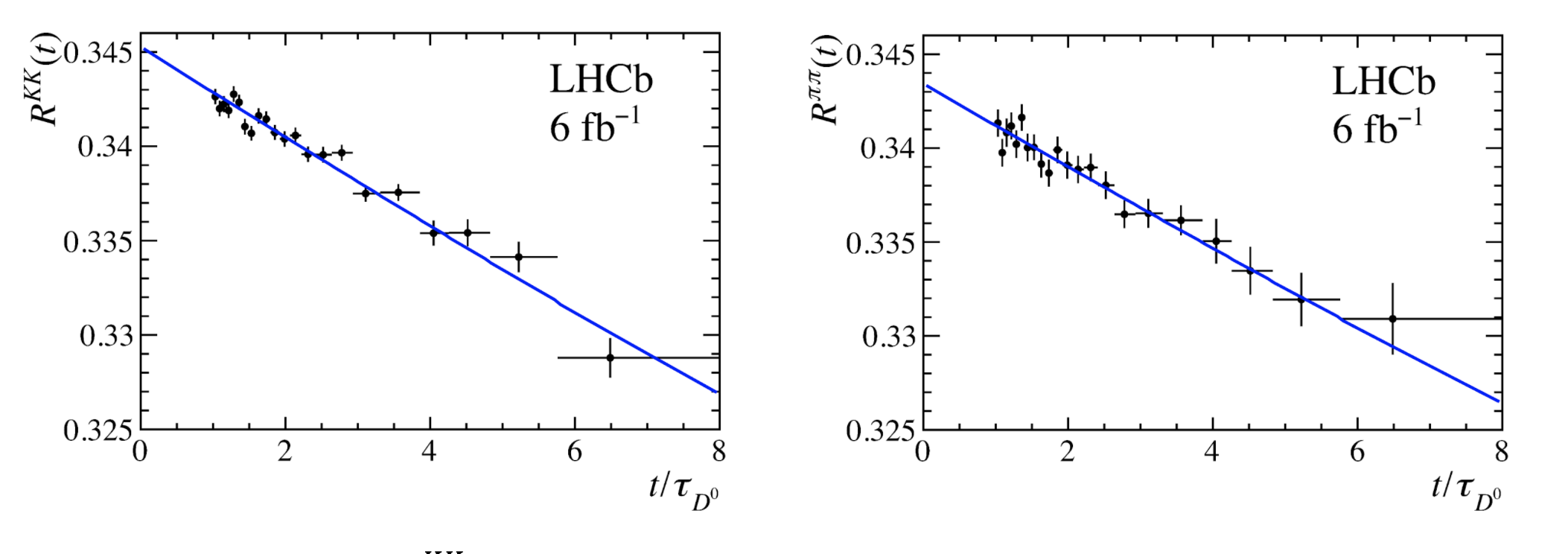
Figure 5: Ratios R^KK_(t) and R^ππ_(t). The slopes of the ratios, estimated in blue, correspond to the measurement of y_CP^KK – y_CP^Kπ and y_CP^ππ – y_CP^Kπ and account for the lifetime difference between D⁰ → K^-K⁺ (D⁰π^-π⁺)and D⁰→K^-π⁺ decays.

The statistical combination of y_CP^KK – y_CP^Kπ and y_CP^ππ – y_CP^Kπ results in y_CP – y_CP^Kπ = (6.96±0.26±0.13)x10^-3, which is four times more precise than previous experimental measurements. Figure 6 compares the new measurement with previous ones.

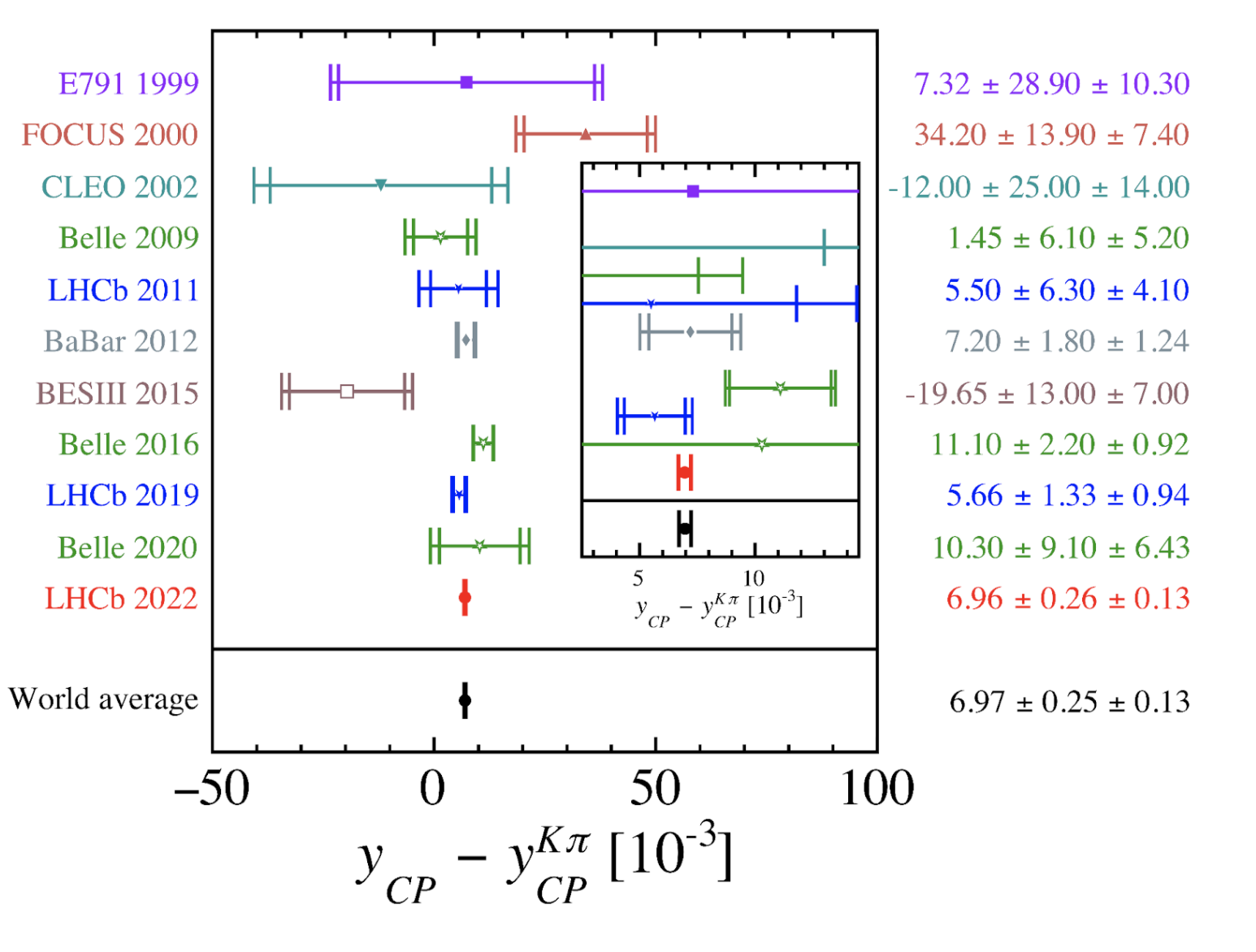
Figure 6: Status of the measurements of y_CP – y_CP^Kπ . The new measurement from LHCb is shown in red (LHCb 2022). The inset plot shows the measurements with a reduced horizontal range. The first uncertainty is statistical and the second systematic.

The new result is used in the combination of LHCb charm measurements performed so far, reducing the uncertainty on y by more than a factor of two, y=(6.46^+0.24_-0.25) x 10^-3.

This exciting result will be included in the next LHCb beauty and charm combination, allowing the experimental knowledge of y to be improved even further.

The recent measurements from LHCb demonstrate that the detector has already achieved better precision than its original design goals. This has been possible thanks to the high quality of the collected data samples and the novel analysis strategies developed to perform measurements seen as extremely challenging, if not impossible, before. When a redesigned LHCb restarts operations later this year the target of sub-degree precision on γ, and the chance to observe CP violation in charm mixing, comes ever closer.