Cornering right-handed neutrinos

Right-handed neutrinos: the missing piece of the puzzle?
The Standard Model (SM) of particle physics is one of the most successful scientific theories ever developed. Together with the theory of General Relativity it can describe most of the observed phenomena in nature at a fundamental level. However, a number of established experimental observations require an extension of the SM. One of them that is also the focus of this article is the observation of neutrino flavour oscillations implying that neutrinos have to be massive (Nobel Prize 2015). Others are related to observations in outer space and e.g. include the mysterious Dark Matter that makes up most mass in the observable universe or the origin of the matter-antimatter asymmetry. While the enormous success of the SM is a reason to celebrate these achievements as an outcome of millenia of research, it also poses a problem: There are very few hints guiding scientists how to find out how the SM should be embedded into a more fundamental theory of nature.
Neutrino oscillations are the only direct evidence for the existence of BSM physics, neutrinos may be a good starting point when looking for clues to the other “big questions”. When searching for possible missing pieces in the SM, one immediately stumbles over the fact that all fermions in the SM are known to exist with both, left- and right-handed chiralities - except the neutrinos. Moreover, the right-handed partners of fermions are crucial to give them masses via the so-called Higgs mechanism in the SM. Hence, introducing right-handed neutrinos (RHN) seems to be a straightforward way to explain the observed neutrino masses [1].
Right-handed neutrinos, if they exist, are different from other SM: They do not “feel” the fundamental forces of nature except gravity, which has also earned them the name “sterile neutrinos”. This not only makes it extremely difficult to detect them, but also implies that the symmetries of the SM permit them to have an additional mass therm, known as Majorana mass, which causes them to be their own antiparticles, a property that would be unique with respect to the so far known particles. In that case, the left-handed neutrinos are inherently massless and feel the weak force, while the right-handed neutrinos have a mass M and do not have interactions with other particles. The Higgs mechanism introduces a quantum mechanical mixing between these two states that can be parameterised by a small mixing angle θ. The generation of neutrino masses in this way is known as the seesaw mechanism and can then be pictured as a sort of deal between the left- and right-handed neutrinos: after the mixing, the SM neutrinos receive a small mass ~M θ², while the heavy sterile neutrinos feature a θ-suppressed weak interaction that makes it possible to detect them. In this picture, heavy neutrinos exhibit three mixing angles θe, θμ and θτ that quantify its weak interaction with the three SM generations of particles. The set {M, θe, θμ,θτ} is a convenient way to parameterise the impact of a given heavy neutrino on different observations. Understanding the possible ranges of the above parameters is key for experimental searches both at collider and fixed-target or astrophysical experiments. In the following we discuss our results from a global fit using a so-called global fit [2].
GAMBIT: a powerful tool to corner them
A key experimental goal, for future experiments, remains the full exploration of the boundaries of the parameter space that is not yet probed and excluded by existing experiments. To address this challenge, we opted for a global fit exploring the possible ranges of the parameters space using the so-called Frequentist statistical approach. Frequentist methods are well known among the particle physics community. The reason for this is that the alternative Bayesian method does not automatically have a built-in mechanism for false positive rates of detections, which play a critical role in defining the statistical significance of a detection. There is a second, perhaps more important reason that makes frequentist approaches a powerful tool. A Bayesian approach requires to define a priori probabilities (in a sense our beliefs) on the model parameter space. However, such priors assumptions depend in general on the actual realisation of a specific model that includes right-handed neutrinos, the so-called “ultraviolet completions”. Depending on the UV completion, regions of the parameter space that appear in one model highly unlikely become the favoured regions in another one, through the presence of additional symmetries. This highlights the fact that Bayesian inference is ultimately about understanding what are the most plausible parameters, given some priors and observations? However, a Frequentist approach is technically much more akin to an optimization task, where we are interested in the observational validity of a single model parameter. This is what makes it suitable for the question that we asked regarding the existence of right-handed neutrino, given the most optimistic configuration of all other model parameters. No priors enter the discussion at any point, and both the virtue and drawback of the approach is that highly tuned regions of the parameter space are not penalized.
It should be noted that in our analysis, we were mostly interested in obtaining prior-independent results. However, performing a formally correct full-fledged Frequentist analysis would have required to treat all observational inputs in our analysis in a fully Frequentist way. This usually means that rates of experimental results have to be known as function of the model parameters - an endeavour that in the best case scenario requires running simulations and in many other cases would have been not possible at all given the limited information that many experiments provide. We hence used an approximate Frequentist approach, which preserves the prior-independence of the results, but makes use of established asymptotic properties of the profile likelihood-ratio test statistic in order to define confidence levels and intervals. Given the vast parameter space that we wanted to explore, the relatively small errors made through this approximation were acceptable.
The main technical challenge of the analysis was then indeed a highly non-convex optimization task. The large parameter space of a model with three right-handed neutrinos requires smart sampling techniques to exhaustively explore all interesting regions. Furthermore, many experimental searches for right-handed neutrinos cover overlapping slices of the parameter space, which requires a proper statistical combination of all constraints via the combination of likelihood functions. In order to simultaneously satisfy all conditions we employ the statistical inference tool GAMBIT (the Global and Modular BSM Inference Tool) is an open-source global-fitting package that contains extensive calculations of observables and likelihoods in particle and astroparticle physics [3].
Complementarity of experiments: A multi frontier approach
After choosing the right statistical tool, the next step is to think of the experimental observations that could imply the existence of right-handed neutrinos and hence constrain the parameter set {M, θe, θμ, θτ}. The strongest constraint arises from the requirement to explain the tiny neutrino masses and the mixing in between their flavour states. The mass of the lightest neutrino, mν0, which can be primarily electron-flavoured (so-called normal hierarchy), or tau-flavoured (inverted hierarchy), comes from effects that neutrinos in the early universe impact the cosmic microwave background and on the formation of structures in the universe [4]. In the future this can be also measured in the KATRIN [5] experiment. The lightest neutrino mass still can range from 0 to the highest value allowed from cosmological observations, m<0.037 eV [10]. The lightest neutrino mass imposes a lower bound on the total mixing of the active and sterile neutrinos, U²=Ue²+Uμ²+Uτ², with Ue²=|θe|² etc. being the flavor specific mixing, as shown in Figure 1.
Besides affecting the properties of the active neutrinos, right-handed neutrinos can be directly searched for at different experiments covering various energy ranges. At low energy scales (up to 450 MeV), decays of light mesons such as pions and kaons (e.g. π+ -> e+ ν or K+ -> μ+ ν), have been studied by the PIENU, PS-191 and E949 experiments [6] constraining the mixing parameters Ue² or Uμ². For intermediate energy scales (up to 3 GeV), the RHN production in heavy flavoured decays was e.g. analysed by the CHARM, LHCb and NuTeV experiments [7]. At high energy scales (up to 1.2 TeV), the mixing is constrained via decays of Z and W bosons with the most precise measurements performed by DELPHI at LEP and recently by the ATLAS and CMS experiments at the LHC [8].
As RHNs would modify the weak interactions of the neutrinos in the SM, they are also expected to alter all processes involving neutrinos. Hence their properties can be additionally tested in an indirect manner. In this context, we considered constraints coming from the measurement of electroweak precision observables (connected to the W and Z bosons), as well as from bounds on lepton flavour violation and lepton universality processes. These processes are being constantly probed by the LHC experiments. RHNs would also have an indirect impact on the CKM matrix, which describes the mixture of the SM quarks. Usually the elements of this matrix are extracted from experiments involving leptons under the assumption of no right-handed neutrinos. Their presence, however, could manifest via apparent unitarity violation of the CKM matrix that we considered in our analysis. In addition, we have considered constraints from neutrinos double-beta decay and Big Bang nucleosynthesis [9]. The latter sets an upper limit on the lifetime of the right-handed neutrino and hence a lower bound on U².
Putting everything together -- the most comprehensive global fit to date
We considered the mass range for the right-handed neutrinos between 60 MeV (below which the existence of heavy neutrinos is practically ruled out by cosmology [10]) and 500 GeV. The statistical combination of all the constraints mentioned above results in a combined likelihood function that stores information about the capability of each parameter point for matching the data. In Figure 1, we show the profile log-likelihood ratio (relative to the best fit point) for values of the mass of any right-handed neutrino in the range [0.06, 500] GeV and its total coupling to left-handed neutrinos in the range [10-15, 10-1]. The samples used for these plots, as well as useful tables containing the 90% and 95% CL upper limits on the total coupling and the individual flavour couplings, can be found in Zenodo [11]. For the purpose of showing the effect of the various constraints on the likelihood surface we show the capped profile likelihood, which is defined for each of the parameter points to an equal or worse fit than the SM. We show the results only for the normal hierarchy of light neutrino masses, unless otherwise stated, as most of the results are agnostic about their particular ordering
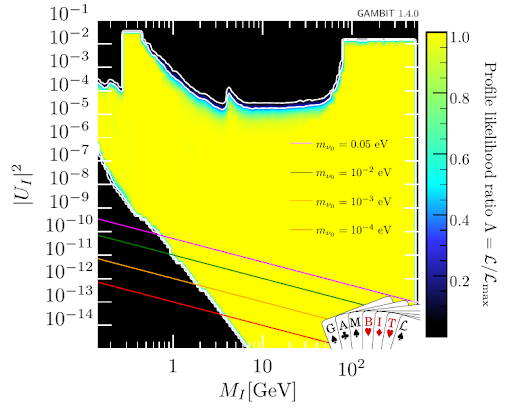
Figure 1: Profile log-likelihood ratio with 1σ and 2σ confidence intervals (white contours) for the mass of one right-handed neutrino and its total coupling. Coloured lines mark the lower limit on the coupling for fixed values of the lightest left-handed neutrino mass mν0.
The results of Figure 1 show the combined exclusions from direct detection experiments as an upper bound on the total coupling between left- and right-handed neutrinos. The lower limit in Figure 1 arises from constraints from Big Bang Nucleosynthesis, as right-handed neutrinos with too small couplings will not decay in the early universe before the formation of primordial elements and affect their measured abundance today. The colored lines correspond approximately to the seesaw limit for different masses of the lightest neutrino, i.e. the lower limit on the coupling required by a minimum value of the lightest neutrino mass. In the massless lightest neutrino limit, no lower bound exists.
Figure 2: Flavour mixing pattern for different upper limits on the lightest neutrino mass in the normal (left) and inverted hierarchy (right). 1σ (solid) and 2σ (dashed) contours are shown for each of the scenarios.
As visible in Figure 1, the lower limit on the total coupling depends strongly on the value of the lightest neutrino mass. In addition, the flavour mixing pattern is also strongly dependent on this value. This can be seen in Figure 2, where we present the allowed region for the normal and inverted hierarchy for various upper limits on the lightest neutrino mass. For the lightest neutrino mass of around 10 meV, there is almost no constraint on the flavour mixing pattern. However, if we go to smaller masses, the allowed ellipse gets significantly reduced. For masses lighter than 0.01 meV the limit saturates and the allowed region of flavour mixing patterns remains the same.
Conclusion and future perspectives
What the above results mean for future experimental strategies in searching for right-handed neutrinos? Current searches for right-handed neutrinos have not found evidence yet, but have set strong constraints on their properties. In this work we have presented the most comprehensive global study of those properties, such as mixings, masses and the flavour mixing pattern. Future searches from experiments currently in development will change this picture significantly, as their increased sensitivity will probe yet unexplored parameter regions, in particular small values of the coupling between left and right-handed neutrinos. Figure 3 shows the future sensitivity of various planned experiments and the exclusion limits they will set on the coupling of RHNs to muon-flavoured ordinary neutrinos.
Figure 3: Sensitivity of future experiments looking for right-handed neutrinos. Grey shaded regions mark the current exclusion limits. Solid lines show the limits on the coupling of the right-handed neutrinos to muon-flavoured left-handed neutrinos. In addition the FCC limit can be further extended by addition of HADES like detectors [12].
This work showcases the benefit of using global fitting tools such as GAMBIT and proper statistical methods. As opposed to conventional methods, global fits combine all constraints in a proper statistical manner and thus report more correct confidence intervals. Rigorous combination of likelihood functions will be crucial in the light of future searches as depicted on Figure 3. Many constraints overlap in a considerable range of the parameter space, and the combined exclusion (or discovery potential) will be larger than their individual one. It can be seen that the planned experiments at FCC, offer one of the most promising paths for hunting the RHNs. The proposed FCC experiments have the potential to probe RHN in a direct way in a large mass range as well as measuring precisely the electroweak parameters that constrain the RHNs.
References
[1] P. Minkowski, Phys. Lett. B 67, 421 (1977); M. Gell-Mann, P. Ramond und R. Slansky, Conf. Proc. C 790927, 315 (1979); R. N. Mohapatra und G. Senjanovic, Phys. Rev. Lett. 44, 912 (1980); T. Yanagida, Prog. Theo. Phys. 64, 1103 (1980); J. Schechter und J. W. F. Valle, Phys. Rev. D 22, 2227 (1980
[2] M. Chrzaszcz et. al., A frequentist analysis of three right-handed neutrinos with GAMBIT, Eur. Phys. J. C 80 (2020) 569, [arXiv:1908.02302].
[3] GAMBIT Collaboration: P. Athron, C. Balázs, et. al., GAMBIT: The Global and Modular Beyond-the-Standard-Model Inference Tool, Eur. Phys. J. C 77 (2017) 784, [arXiv:1705.07908]. 40. GAMBIT Scanner Workgroup
[4] Julien Lesgourgues, Sergio Pastor, Massive neutrinos and cosmology, Phys.Rept. 429 (2006) [arXiv: astro-ph/0603494]
[5] KATRIN Collaboration, Improved Upper Limit on the Neutrino Mass from a Direct Kinematic Method by KATRIN, Phys.Rev.Lett. 123 (2019) no.22, 221802 [arXiv:1909.06048]
[6] PIENU: M. Aoki et. al., Search for Massive Neutrinos in the Decay π → eν, Phys. Rev. D84 (2011) 052002, [arXiv:1106.4055]; PIENU: A. Aguilar-Arevalo et. al., Improved search for heavy neutrinos in the decay π → eν, Phys. Rev. D97 (2018) 072012, [arXiv:1712.03275]; PS-191: G. Bernardi et. al., Further limits on heavy neutrino couplings, Phys. Lett. B203 (1988) 332–334; E949: A. V. Artamonov et. al., Search for heavy neutrinos in K+ → µ +νH decays, Phys. Rev. D 91 (2015) 052001, [arXiv:1411.3963]. [Erratum: Phys. Rev. D 91,no.5,059903(2015)].
[7] CHARM: F. Bergsma et. al., A Search for Decays of Heavy Neutrinos in the Mass Range 0.5-GeV to 2.8-GeV, Phys. Lett. B 166 (1986) 473–478; J. Orloff, A. N. Rozanov, and C. Santoni, Limits on the mixing of tau neutrino to heavy neutrinos, Phys. Lett. B550 (2002) 8–15, [hep-ph/0208075]; NuTeV, E815: A. Vaitaitis et. al., Search for neutral heavy leptons in a high-energy neutrino beam, Phys. Rev. Lett. 83 (1999) 4943–4946, [hep-ex/9908011]; LHCb: R. Aaij et. al., Search for Majorana neutrinos in B− → π +µ −µ − decays, Phys. Rev. Lett. 112 (2014) 131802, [arXiv:1401.5361].
[8] DELPHI: P. Abreu et. al., A Study of the reaction e +e − → µ +µ −γ (ISR) at LEP and search for new physics at annihilation energies near 80-GeV, Z. Phys. C 75 (1997) 581–592; ATLAS Collaboration: G. Aad et. al., Search for heavy Majorana neutrinos with the ATLAS detector in pp collisions at √ s = 8 TeV, JHEP 07 (2015) 162, [arXiv:1506.06020]; CMS Collaboration: A. M. Sirunyan et. al., Search for heavy neutral leptons in events with three charged leptons in proton-proton collisions at √ s = 13 TeV, Phys. Rev. Lett. 120 (2018) 221801, [arXiv:1802.02965]; ATLAS: G. Aad et. al., Search for heavy neutral leptons in decays of W bosons produced in 13 TeV pp collisions using prompt and displaced signatures with the ATLAS detector, arXiv:1905.09787;. CMS: C. Collaboration, Search for heavy Majorana neutrinos in the same-sign dilepton channel in proton-proton collisions at √ s = 13 TeV; CMS: A. M. Sirunyan et. al., Search for heavy Majorana neutrinos in same-sign dilepton channels in proton-proton collisions at √ s = 13 TeV, JHEP 01 (2019) 122, [arXiv:1806.10905].
[9] A. D. Dolgov and F. L. Villante, BBN bounds on active sterile neutrino mixing, Nucl. Phys. B 679 (2004) 261–298, [hep-ph/0308083].
[10] P. Hernandez, M. Kekic, J. Lopez-Pavon, 𝑁eff in low-scale seesaw models versus the lightest neutrino mass, Phys.Rev. D90 (2014) no.6, 065033IFIC-14-25, [arXiv:1406.2961]. Aaron C. Vincent, Enrique Fernandez Martinez, Pilar Hernández, Massimiliano Lattanzi, Olga Mena, JCAP 1504 (2015) 006IFIC-14-53 [arXiv:1408.1956]
[11] https://zenodo.org/record/3842838
[12] M. Chrzaszcz, et. al. , HADES: A long lived particle detector concept for the FCC-ee or CEPC, e-Print: 2011.01005 [hep-ph]
