Among the sciences, particle physics has the luxury of having a well established theoretical basis. Often we focus on the elementary particles and model them mathematically with quantum field theories like the Standard Model. In order to compare with data, we must also model the additional radiation, decays, hadronization, and the interaction of particles with the detectors. We describe these effects with sophisticated computer simulations like Pythia or Geant4.

The simulation allows us to mimic what we might observe in the experiments for any values of the theoretical parameters, which typically correspond to the masses and couplings of the particles or the Wilson coefficients of an effective field theory. Feynman famously said “What I cannot create, I do not understand”… … but does being able to create synthetic data imply understanding? Not really.

Measurements need the likelihood function... but we can almost never compute that 

Ultimately, our goal is not to turn models and parameter values into synthetic data, which computer simulations are excellent at. Rather, we aim to extract laws of physics and the values of theoretical parameters from observed data. In a sense, the inference step of the scientific method proceeds along the inverse direction of the forward operating mode of particle physics simulators.

As Robert Cousins recently explained in this newsletter, the central object for inference (hypothesis tests, confidence intervals, and parameter measurements) is the likelihood function: the probability density of the observed data, evaluated as a function of the theory parameters. The likelihood function allows us to find the best-fit points for theory parameters (through maximum likelihood estimators) as well as to put error bars on them (confidence regions from likelihood ratio tests).

Now here is the problem: we cannot actually compute the likelihood function when we describe a process with simulators and the observed data is high-dimensional! We can write down the likelihood function symbolically, but evaluating it would require integrating over all possible event histories that lead to the same observed data. Since simulating an event with a realistic detector simulation easily involves tens of millions of random variables (the different random choices made in the simulation of a single event), this is an integral over a ten-million-dimensional space. So while we can use Monte Carlo to sample from this distribution, integrating it is clearly impossible, leaving us with no way of evaluating the likelihood function directly. 

Is this the way?

Traditionally, particle physicists have addressed this issue by reducing the high-dimensional data collected in particle collisions to a single kinematic variable. For instance, when looking for signs of the Higgs boson decaying into four leptons, one would only consider the invariant mass of the reconstructed four-lepton system. After reducing the high-dimensional data to this single kinematic variable, one can approximate the likelihood function by filling histograms with simulated and observed data. In particle physics jargon, this is known as analyzing a (single) differential cross section. In statistics, this kinematic variable – what’s on the x axis of the histogram – is called a summary statistic. 

This approach is so established in particle physics that it is often taken for granted. This is understandable since the reduction of the data to a summary statistic makes inference possible in the first place. It also has been very successful (we have after all found the Higgs boson and determined its couplings and mass in this way).

Nevertheless, reducing the data to a single kinematic variable is in many cases not optimal: it discards information, leading to weaker analysis results than necessary. Just analyzing the four-lepton mass variable, for instance, makes it very hard to constrain indirect effects of new physics such as effective field theory operators. Instead, we really want to analyze the fully differential cross section, that is, the high-dimensional data without having to reduce it to a single kinematic variable. This is particularly true for the legacy measurements of the LHC.

Machine learning to the rescue

In the last few years, several new methods have been developed that let us solve this problem and analyze high-dimensional particle physics data without requiring reducing this data to a single kinematic variable. These methods are powered by machine learning models like neural networks and benefit from the ongoing revolution in deep learning.

Machine learning of course has many facets. Well-known applications include classification (answering which of a set of discrete categories a sample belongs to) and regression (linking a sample to a continuous target variable). Then there are generative models like Generative Adversarial Networks (GANs), which can learn to produce synthetic data that mimics some training examples. Themodels and algorithms for these three tasks cannot immediately be applied to the data analysis problem in particle physics. However, as it turns out, we can borrow  and combine ideas from all three of them to create powerful inference methods.

The least disruptive of these methods keeps the basic workflow of classic particle physics analysis, but uses a neural network to learn powerful summary statistics. Instead of histograms of the four-lepton invariant mass, the pseudorapidity of a photon, or the azimuthal angle between two jets, one fills a histogram of the output of a specially trained neural network and statistically analyzes this quantity with all the established histogram-based statistical tools. Without going into detail here, one can train a neural network such that its output defines an observable that is proven to be optimal for parameter measurements, i.e. will lead to the strongest possible limits on some parameters, as long as the true parameter point is “close enough” to some reference value (like the Standard Model). This approach is an excellent starting point as it requires only very minor modifications to existing analysis pipelines.

At this point the alert high-energy physicist may be wondering, “We’ve been using machine learning in our analyses for many years. How is this different?”. Typically, LHC analyses use machine learning to classify between signal-like and background-like events. The events classified as signal are then usually analyzed through histograms of standard kinematic observables, though sometimes the neural network output itself is used as a summary statistic. The output of the machine learning models (which in LHC analyses are often neural networks or boosted decision trees) may be great at signal-background discrimination, but they are typically not optimal to measure parameters. The approach we are describing here, on the other hand, directly optimizes the network output so that it has captures all the information needed to infer the value of theory parameters. 

A second, more far-reaching approach is to directly train a neural network to learn the likelihood function or the closely related likelihood ratio function. During inference, we can then use this machine learning model as a surrogate for the simulator. This method consists of three steps: first, we run our suite of simulators with different parameter points as input; second, we train a neural network classifier to discriminate between data from different points; finally, we transform the output of the trained neural network into a proxy of the likelihood ratio, which can then be used  to find best-fit points and exclusion limits. Unlike the simpler approach in which a neural network just defines summary statistics, this method does not just work well in the neighborhood of a reference parameter point, but anywhere in parameter space. Given enough training data)it  can be optimal for parameter measurements, independent of the true value of the parameter point. Essentially the network is learning a multivariate, unbinned likelihood. While this approach is more of a break from the traditional analysis pipeline, it can lead to even more precise parameter measurements. 

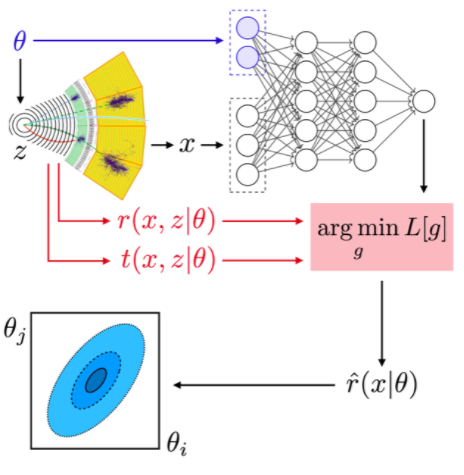
One worry with such approaches is the amount of simulated training data that is needed. As it turns out, we can make the training much more efficient if we do not just treat the particle physics process as a black box, but use our physics understanding of the process implemented inside it. In particular, we can extract matrix-element information from the simulator and use it to augment the training data for the neural networks. This can make the training much more sample efficient, meaning that we need orders of magnitude less simulated data to train the neural networks. This sketch summarizes all the pieces in such an analysis:

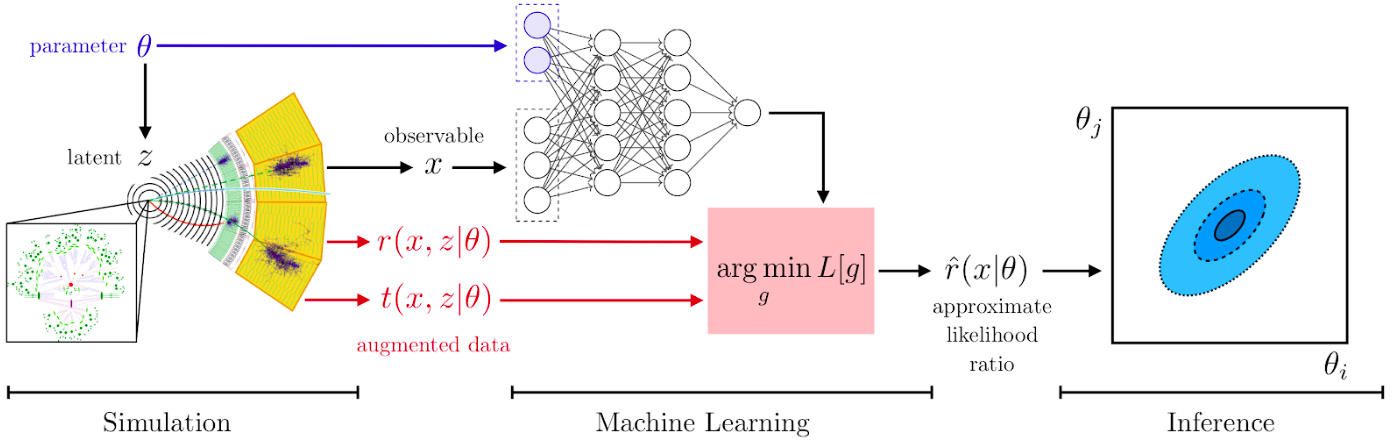
Schematic workflow of machine learning–based inference methods. In the first stage, we simulate events, storing both the event data as well as matrix element weights that can be calculated from the Monte-Carlo truth record. Second, we use the simulated events and matrix element weights to train a neural network to learn the likelihood ratio function. Third, the neural network is used for inference, for instance to determine the best-fit points (maximum likelihood estimators) and limits (confidence sets). From “Constraining Effective Field Theories with Machine Learning”.

These new machine-learning based approaches have much in common with the so-called Matrix Element Method, which also aims to provide an unbinned, multivariate likelihood function for the data. However, the Matrix Element Method requires summarizing shower and detector effects with transfer functions, while these machine learning–based inference methods require no simplifications to the underlying physics and support state-of-the-art shower and detector simulations. The machine learning–based approaches are also “amortized”: after the upfront computational cost of generating training data and training the neural networks, the likelihood for new events can be evaluated in microseconds. But most importantly, they allow us to get more information out of observed data. In several early phenomenological studies, these approaches led to substantially  more precise measurements and better limits in searches. For instance, the following plot shows the expected limits on two EFT parameters in the production of a Higgs boson together with a W boson at the LHC:

Expected limits on two EFT parameters C_HW and C⁽³⁾_HQ in WH precision measurements. The red dashed and green dash-dotted lines show the expected limits from a traditional analysis based on two kinematic variables. The solid blue line shows the expected limits from a machine learning–based analysis as discussed here. It is substantially tighter around the Standard Model point (the origin in this figure), showing that the methods presented here can lead to more sensitive measurements.
From "Benchmarking simplified template cross-sections in WH production".

Someone interested in these methods does not have to work through all the math themselves or implement the algorithms from scratch. The Python library MadMiner implements them and makes it straightforward to apply them to most particle physics measurements. MadMiner wraps around MadGraph 5, Pythia 8, and Delphes, providing the ingredients for a typical phenomenological study. There is even an online tutorial. It should be noted that this approach is also compatible with a full detector simulation like Geant4: the necessary information can just be passed through the detector simulation similar to the weights used to assess uncertainty in the parton distribution functions. Nevertheless, this will still require some investment in the experiments’ simulation software.

We describe and discuss these methods and their software implementation in more detail in this chapter for an upcoming book on “AI for Particle Physics”.

The analysis methods presented here have so far been applied in phenomenological studies of Higgs precision measurements in vector boson fusion, in WH production, and in ttH production, as well as ZW measurements and the search for massive resonances decaying into dijets. The new machine learning–based techniques consistently led to more sensitive analyses than traditional histogram-based approaches. Using matrix-element information efficiently allows us to cut down on the number of simulations we need. With constant progress in machine learning as well as the development of software packages making the application of these methods easier, the application of these new simulation-based inference techniques to data collected at the LHC experiments seems imminent.

A world of simulation-based inference

Particle physics is far from the only field that uses complex simulators to make predictions for the data, and therefore faces challenges in modelling the likelihood function. The same issue appears in fields from neuroscience to ecology, from systems biology to epidemiology, from climate science to cosmology, and so on. The term simulation-based inference (our preferred term) or likelihood-free inference is used to refer to the general class of techniques being used to address these problems. This common framing of the problem serves as a lingua franca and  presents an opportunity for scientists from different domains, statisticians, and computer scientists to develop analysis methods together and to learn from each other.

Simulation-based inference is an active and exciting area of interdisciplinary research and an area where particle physics is contributing ideas that are impacting other fields. Progress is happening mostly along three broad trends. We already mentioned the revolution in machine learning, which lets us tackle higher-dimensional data efficiently. The second trend is the tighter integration of simulation and inference, the efficient use of matrix-element information in particle physics is one example of this. Finally, active learning describes methods that use past knowledge and observed data to simulate more data exactly in the regions of parameter space where it is expected to be most useful, improving the sample efficiency even more. 

In an article recently published by the Proceedings of the National Academy of Sciences, we discuss simulation-based inference broadly, review recent progress along these three trends, and provide an opinionated outlook on the future of this exciting research area.