The quest for new physics at the LHC is entering a new phase: the experiments are designing new strategies to target potential deviations from the Standard Model (SM) predictions in a systematic way, to complement the traditional “bump hunts” and, potentially, extend their sensitivity to mass regions beyond the collider reach.

This kind of new physics signature has been long known and searched for. For instance, constraints on anomalous couplings of the gauge bosons were set already at LEP. Today, thanks to modern Effective Field Theory (EFT) techniques developed in the past decade,  these studies can be organized in a coherent, unified program. The key innovation is that ad-hoc parameterizations and assumptions are replaced by a common theory framework: the so-called Standard Model Effective Field Theory  (SMEFT). This will allow to extend indirect searches to a wide range of processes, and to derive results that are better defined and apply to a vast class of beyond-SM (BSM) scenarios.  The adoption of the SMEFT language will also facilitate the re-interpretation of LHC measurements in the future.  

An effective plan

In essence, an EFT is a field theory that approximates another one in a specific dynamic regime. The concept is so intuitive that, in fact, its roots were planted even before Quantum Field Theory was formulated.The earliest example dates back to 1933, when Enrico Fermi proposed a model of beta-decays [1] based on a local interaction among four spin ½ particles: a neutron, a proton, an electron and a neutrino, that at the time was just an hypothetical particle. Today we know that this interaction actually involves the nucleons’ fundamental constituents, the quarks, that it is mediated by the W boson and much more. Fermi’s theory ignored all this, but still proved very successful in describing beta decays. The reason is that the typical energy E exchanged in these processes is always significantly smaller than the W mass: in this limit, the weak interactions effectively become point-like. Effects sensitive to the finer SM structure are suppressed by additional powers of (E/m_W) << 1, and can thus be revealed only with a high experimental resolution. 

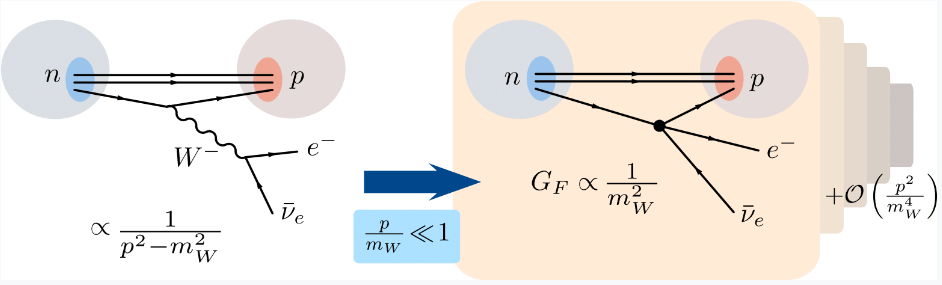
Figure 1. Pictorial view of the Fermi theory example. For transferred energies much smaller than the W mass, the weak interactions effectively behave as if they were point-like, and they scale as GF ~ 1/mW².

Fermi’s theory is the most classic example of “bottom-up” EFT. In this approach,  the effective theory is formulated based only on low-energy assumptions, i.e. by specifying the dynamical fields and symmetries (p,n,e,v and QED) and the Lagrangian contains all possible interaction terms consistent with these choices, weighted by free parameters called Wilson coefficients. By construction, this theory can describe the effects of any possible UV scenario compatible with its working assumptions. Different heavy sectors simply correspond to different values and patterns in the Wilson coefficients. This implies that, by measuring the EFT parameters, one can reconstruct the main properties of the underlying physics.  In Fermi’s example, an EFT analysis of the beta decay rates and spectra is sufficient to infer, for instance, the electric charge and mass scale of the mediating particle (the Wilson coefficient is GF = 1/√2 v²), as well as the universality and chirality of its interactions.

The SMEFT is the EFT obtained choosing the SM fields and symmetries as building blocks. It approximates a vast class of BSM scenarios, that need to fulfill only a minimal set of requirements. Perhaps the most restrictive one is that all new particles are assumed to be significantly heavier than the electroweak (EW) scale v ~ 246 GeV. This means that, strictly speaking, the SMEFT cannot describe the physics of a light QCD axion or of light sterile neutrinos, although extensions of the theory (e.g. νSMEFT) are of course possible.

Within its applicability regime, the SMEFT provides a very powerful parameterization of potential deviations from the SM. It is a well-defined field theory (renormalizable order by order), a universal language that applies to all processes and an exhaustive classification of all possible BSM effects. This makes it a natural framework to organize indirect searches systematically.

The last decade has seen a number of substantial developments in the formulation of the SMEFT. Why now? The motivation for this interest is twofold: on the one hand, the lack of experimental indications in favor of a given BSM model makes the SMEFT’s broad applicability clearly appealing. Moreover, resonance searches are consistent with the absence of exotic particles up to the TeV scale, in accordance with the SMEFT working hypotheses.

At the same time, collider physics is entering a precision era: in the next two decades the LHC experiments will collect more and more data (up to 20 times the current data sets) but won’t access much higher center-of-mass  energies. Even for the facilities that have been proposed as successors of the HL-LHC, many feature a design that favors precision over energy. Precise measurements and EFTs go hand-in-hand: for EFT analyses to be conclusive, precision is imprescindible. Conversely, precise measurements require a solid EFT framework in order to be interpreted consistently in a global BSM perspective. Arguably, the SMEFT infrastructure is always valuable whenever accurate measurements are available, because it allows to maximize the information extracted from the dataset and to store it in a well-defined and easily re-interpretable manner. This information is complementary to the results of direct searches, and can be sensitive to scales beyond the energy reach of the collider. 

The SMEFT challenge

This plan is not without its challenges. A first hurdle in the realization of the EFT program is that the observation of  SMEFT effects requires a precision of a few % around SM resonance peaks and 10-20 % in the high energy tails, with a large variability between processes. Both these targets are ambitious for the LHC, but likely attainable at the HL-LHC with significant improvements on both the experimental and theoretical sides.

At the same time, the breadth of scope of the SMEFT comes at the price of a large number of parameters: the leading deviations from the SM are induced by operators of dimension 6. At this order there are 2499 independent real parameters. The number can be reduced to ~80 if the flavor structure is maximally simplified. A significant subset of these parameters contributes to many processes involving all sorts of SM particles. Conversely, any given process typically receives corrections from 10-20 different operators, some of which lead to fully degenerate effects.

This poses a challenge for modeling BSM signals,  as well as for the interpretation of experimental measurements. No individual analysis can constrain independently all the EFT parameters contributing to a process of interest.  On the other hand, a reduction a priori of the parameter space would inevitably introduce a bias. The preferred strategy is then to combine measurements of multiple processes, to constrain a large number of degrees of freedom simultaneously, in a global statistical analysis.

Due to the complexity of the SMEFT, this combination should ideally include measurements from different  sectors, for instance EW, Higgs and top quark processes. The more inclusive is the global analysis, the more reliable and general the results can be. This is an unprecedented challenge for the LHC experiments, and it will require, for instance, a set of common definitions for the modeling of both signals and backgrounds, and a consistent treatment of theoretical uncertainties. Last summer, the LPCC established a dedicated working group, the LHC EFT WG [2], that will operate as a platform for the coordination activities.

Status and outlook

The ATLAS and CMS experiments have already begun addressing some of these challenges: an increasing number of analyses of top quark, Higgs and EW processes report an EFT interpretation of their results. First steps towards combinations within each sector have also been taken already: for instance, already 3 years ago, the Top WG released a document with recommendations for SMEFT analyses of top quark processes [3]. 

At present, much effort is being put into developing optimal strategies for handling the large number of parameters in the signal modeling and in the statistical analyses. The ATLAS Collaboration has carried out studies for the specific case of Simplified Template Cross Sections (STXS) for Higgs measurements [4] and last year it presented the results of the first global analysis of this class of observables, using its full Run-2 data set and including 16 SMEFT operators [5]. The same number of degrees of freedom (although of different nature)  has been constrained more recently in the first global analysis of top quark production processes by the CMS Collaboration [6].

Figure 2: Summary of observed constraints on SMEFT parameters from a global analysis of STXS measurements by ATLAS. The ranges shown correspond to 68% (solid) and 95% (dashed) confidence level intervals, where all other coefficients and all nuisance parameters were profiled. For more details see: ATLAS-CONF-2020-053.

Figure 3: Summary of observed constraints on SMEFT parameters from a global analysis of top quark production processes by CMS. The ranges shown correspond to 1σ (thick line) and 2σ (thin line) confidence intervals (CIs). Solid lines correspond to the other WCs profiled, while dashed lines correspond to the other WCs fixed to the SM value of zero.  For more details see: CMS-TOP-2019-001.

Both ATLAS and CMS results indicate that, for some directions in parameter space, the current sensitivity reaches already into the multi-TeV range in terms of BSM scales, which is in line with the findings of a number of theory studies. The latter also showed that several bounds are expected to improve significantly with the inclusion of (multi)-differential measurements and constraints from other sectors, that help “breaking” poorly constrained directions in the SMEFT parameter space.

In the upcoming months, the ATLAS and CMS experiments will start gearing up for their first “super-combination” that, in the long run, can include up to 50 - 60 free parameters. The LHCb experiment is also likely to take part in this program, contributing in particular with B-physics measurements. It will likely be a long road, along which these analyses will gradually become more sophisticated and more comprehensive. Ultimately, the SMEFT challenge can be won with a community effort, in which theory and experiment join forces to develop the required infrastructure: many contributions are needed, from the reduction of theoretical uncertainties to the selection of optimal observables, from matching techniques to connect the SMEFT to BSM models to the implementation of efficient frameworks for simulations and global statistical analyses.

The SMEFT framework allows to incorporate naturally measurements from non-LHC experiments as well, at least at the level of a phenomenological study. This has been done already for data collected, for instance, at LEP and  Tevatron. The addition of measurements of lower-energy observables, such as electric or magnetic dipole moments (g-2) or meson oscillations and decays, would be crucial for constraining the flavor structure of the SMEFT. New results from upcoming  experiments will also be easily included in the future. In this way, the SMEFT can serve as a flexible theoretical framework for the analysis of HEP measurements and their future re-interpretation.

References

[1] E. Fermi, Tentativo di una teoria dell'emissione dei raggi beta, La Ricerca Scientifica 4 (1933) 491-495

[2] https://lpcc.web.cern.ch/lhc-eft-wg

[3] CERN-LPCC-2018-01

[4] ATL-PHYS-PUB-2019-042

[5] ATLAS-CONF-2020-053

[6] CMS-TOP-19-001