Axion-like-particles (ALPs) are a vast family of hypothetical particles. They are among the most compelling candidates for physics beyond the Standard Model (SM), because their existence is associated to broken symmetries, which are ubiquitous in theories addressing any of the big open questions, from the hierarchy problem to the strong CP problem, from the matter-antimatter asymmetry in the universe to the flavor puzzle. The members of the family are often distinguished based on the nature of the symmetry, so they go under the name of QCD axion, Majoron, flavon, relaxion. Nevertheless, all ALPs share the same fundamental properties: they are electrically neutral, have spin 0, odd parity (they are pseudo-scalars) and tend to be much lighter than the sector they originate from. This last property is key: it implies (i) that ALPs could be very light, enough to be discovered at the LHC or at much lower energy facilities, (ii) that the non-observation of other new particles cannot disprove the existence of ALPs and (iii) that the discovery of an ALP would directly imply the existence of a whole new heavy sector and give important indications as to how it can be accessed. 

It is then unsurprising that the interest in ALPs has been growing significantly in recent times, prompting great advancements on both theoretical and experimental fronts. A plethora of new experiments and strategies to search for these particles have been proposed in the past few years, many of which form part of the Physics Beyond Colliders program at CERN.  The LHC experiments also have much to say about ALPs: most notably, they have privileged access to ALPs interacting with heavy SM particles (i.e. top quarks, W, Z and Higgs bosons), which are hard to probe elsewhere. For instance, some recent developments in the direction of ALP-Higgs interactions were covered in a previous EP newsletter article.

The ATLAS and CMS Collaborations have been looking for ALPs covering mainly two scenarios: where the ALP is light and stable, and it escapes detection leaving a “mono-X” signature (with X = W, Z, H, γ) , or where it is in the GeV-TeV mass range and it decays resonantly into a pair of SM bosons (γγ, WW or ZZ). 

In 2019 it was proposed that a third regime could be exploited, where the ALP is produced non-resonantly [1]. This happens whenever the ALP mediates the production of a particle pair that is much heavier than the ALP itself. For instance, if the ALP has a mass of 1 MeV, it cannot decay into a top-antitop or a ZZ pair, but it can still enhance the production cross-section of these heavy particles via virtual contributions (see the diagrams in Fig.1). This is a purely quantum effect that is normally suppressed for SM particles, but not for ALPs, because the suppression is compensated by a characteristic property of ALP interactions: that they grow with energy. The resulting signal is not a resonance peak, but rather a smooth deformation of the kinematic distributions of the final state particles (see Fig. 2 below), a phenomenon very similar to the effect of SM Effective Field Theory (SMEFT) operators (though the SMEFT models new physics that is too heavy to be resonant, rather than too light as in the ALP case).

The main advantage of non-resonant ALP signatures is that their signal cross sections and kinematical distributions are largely independent of the ALP mass and of the ALP decay width. The only requirement is that the ALP always transfers an amount of energy much larger than its mass (and in particular the resonant regime is kinematically forbidden): in the case of a ZZ pair production, ALPs of any mass will give the same signal, provided they are lighter than about 100 GeV. This allows the experiments to probe vast regions of the ALP parameter space at once, which are typically complementary to those explored by resonant searches, as the latter are only sensitive to higher masses (roughly between 1 GeV and a few TeV).

Figure 1. Representative Feynman diagrams leading to non-resonant ALP signals in the production of ZZ and top-antitop pairs via gluon fusion (first two from left) and in Vector Boson Scattering (last two). 

The idea of non-resonant searches for ALPs at the LHC was first proposed in the context of inclusive di-boson and top-antitop pair production, where the ALP is produced via gluon fusion [1], see Fig. 1.  Reinterpreting public ATLAS and CMS results for these processes, Refs. [1,2] extracted upper limits on the product of the ALP coupling to gluons with the relevant coupling to dibosons. Last November the CMS Collaboration published a dedicated search that implements the same strategy to the measurement of inclusive ZZ and ZH production [3]. 

In a recent preprint [4], we have proposed to extend the non-resonant approach to measurements of Vector Boson Scattering (VBS). VBS [5] refers to the electroweak production of a pair of electroweak bosons (W, Z, γ) in a parton scattering process whose characteristic signatures are two very energetic jets, well-separated in pseudo-rapidity. Because they are purely electroweak, VBS processes are quite rare in the Standard Model, with a cross section of few femtobarns. Nevertheless, they historically represent an important playground for the study of the electroweak sector. The interest in VBS measurements has considerably grown during Run 2, where the ATLAS and CMS experiments were able to observe several of these processes for the first time, including the production of WW, WZ, ZZ, Zγ and Wγ pairs. VBS measurements are bound to improve significantly in the future: both the Run 3 of the LHC, scheduled to start this year, and the planned High Luminosity LHC (HL-LHC), will offer a wealth of new data that will enable us to move beyond first observations into the domain of precision measurements. The precision program for VBS is quite rich, spanning from SMEFT measurements to the ambitious goal of isolating the transverse and longitudinal components of the W and Z bosons.  

In the context of non-resonant ALP searches, the main advantage of employing VBS measurements is that, here, the ALP signal does not rely on the presence of an ALP-gluon interaction. Thus, even though they have smaller statistics compared to those of inclusive diboson production, VBS measurements allow the extraction of cleaner information about ALP couplings to γ, W and Z bosons. Moreover, the VBS production mechanism allows several different di-boson pairs to be produced already at tree level, which is very convenient because it provides a way to over-constrain the ALP parameter space from many complementary directions (see Fig 3 below).

In our work, we studied non-resonant ALP signals in VBS by reinterpreting public VBS measurements by the CMS Collaboration. We considered 5 different VBS processes, i.e. the production of same-sign WW, WZ [6], ZZ [7], Wγ [8] and Zγ [9] pairs, with all Z bosons decaying to electron or muon pairs, and W bosons decaying into an electron or muon and a neutrino. For each of them, we estimated how the ALP signal would contribute to the quantities measured by CMS. One example is shown in Figure 2.

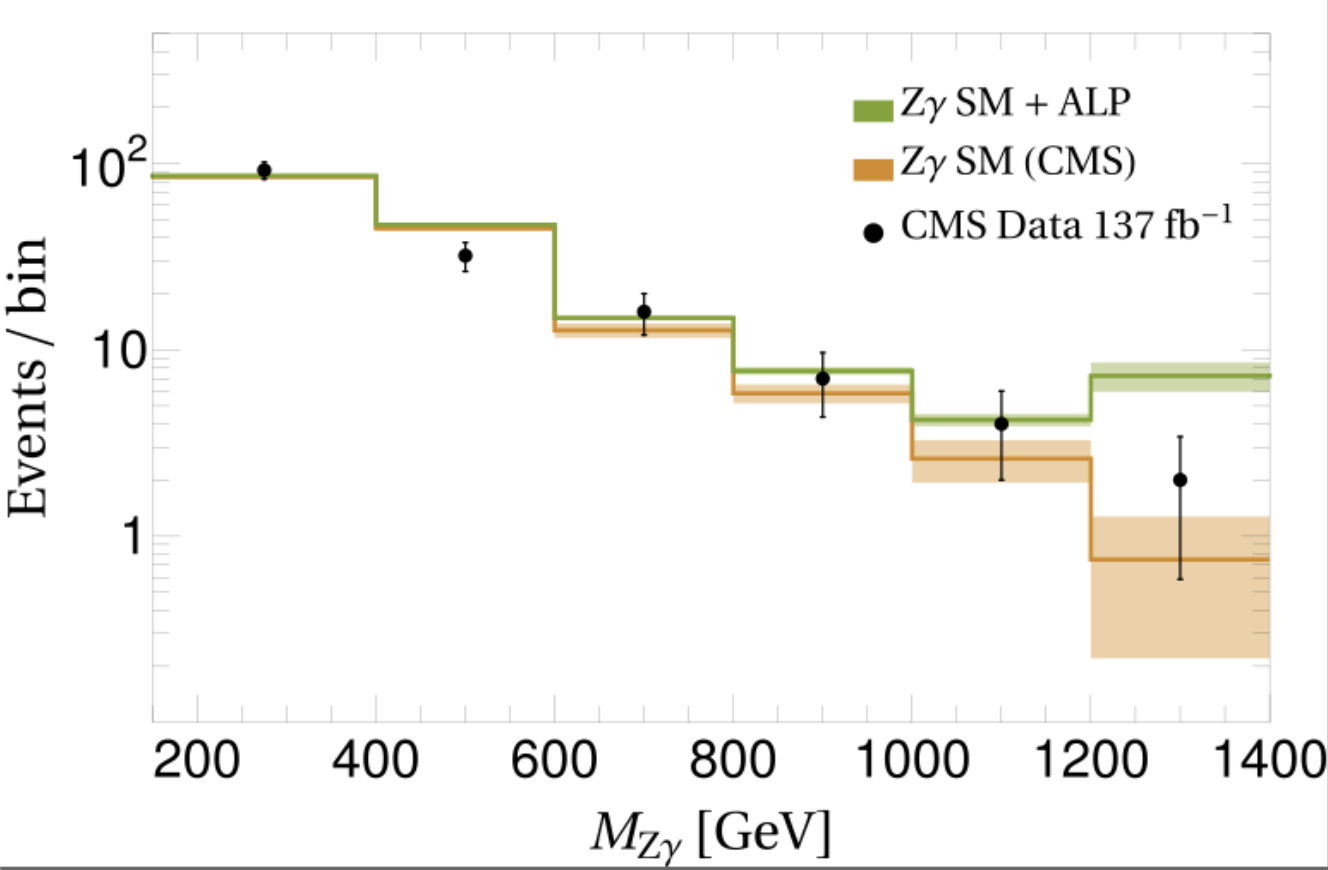
Figure 2. Example of non-resonant ALP signal in VBS: distribution of the invariant mass of the (Zγ) system in the electroweak process q q → j j Z γ. The orange curve and the data points are taken from [9], while the green curve shows the ALP signal for (cW/fa)=(cB/fa)=1/TeV.

The ALP signal depends on 2 theory parameters, that we call (cW/fa) and (cB/fa) to highlight that they are dimensionful, i.e. cW, cB stand for some number, while fa roughly represents the typical mass of the sector the ALP originates from. These two quantities are coupling constants that control the four possible interactions of the ALP to electroweak boson pairs, i.e. to W⁺W^-, ZZ, γγ and Zγ. The operative goal of the study is to measure (or set upper bounds on, in the absence of a signal) (cW/fa) and (cB/fa).

The results of the statistical analysis are shown in Figure 3, for each of the VBS channels individually and for their combination. Since the CMS measurements did not find any significant disagreement between the data and the SM predictions, we can only draw exclusion limits on the ALP couplings. The figure tells us that values of (cW/fa) and (cB/fa) greater than roughly 1/TeV (i.e. the region outside the curves) are not viable, otherwise CMS would have detected a non-resonant ALP signal. It is interesting to observe that the lines have different, complementary shapes for each VBS channel. This happens because the ALP signal is a different function of the two free parameters depending on which boson pair is produced. For instance, the signal in same-sign WW (in red) does not depend at all on (cB/fa). Those in Wγ and WZ do depend on both parameters, but if (cW/fa)=0 the ALP signal completely disappears, independently of (cB/fa). This is why the light and dark blue curves do not close in the vertical direction. 

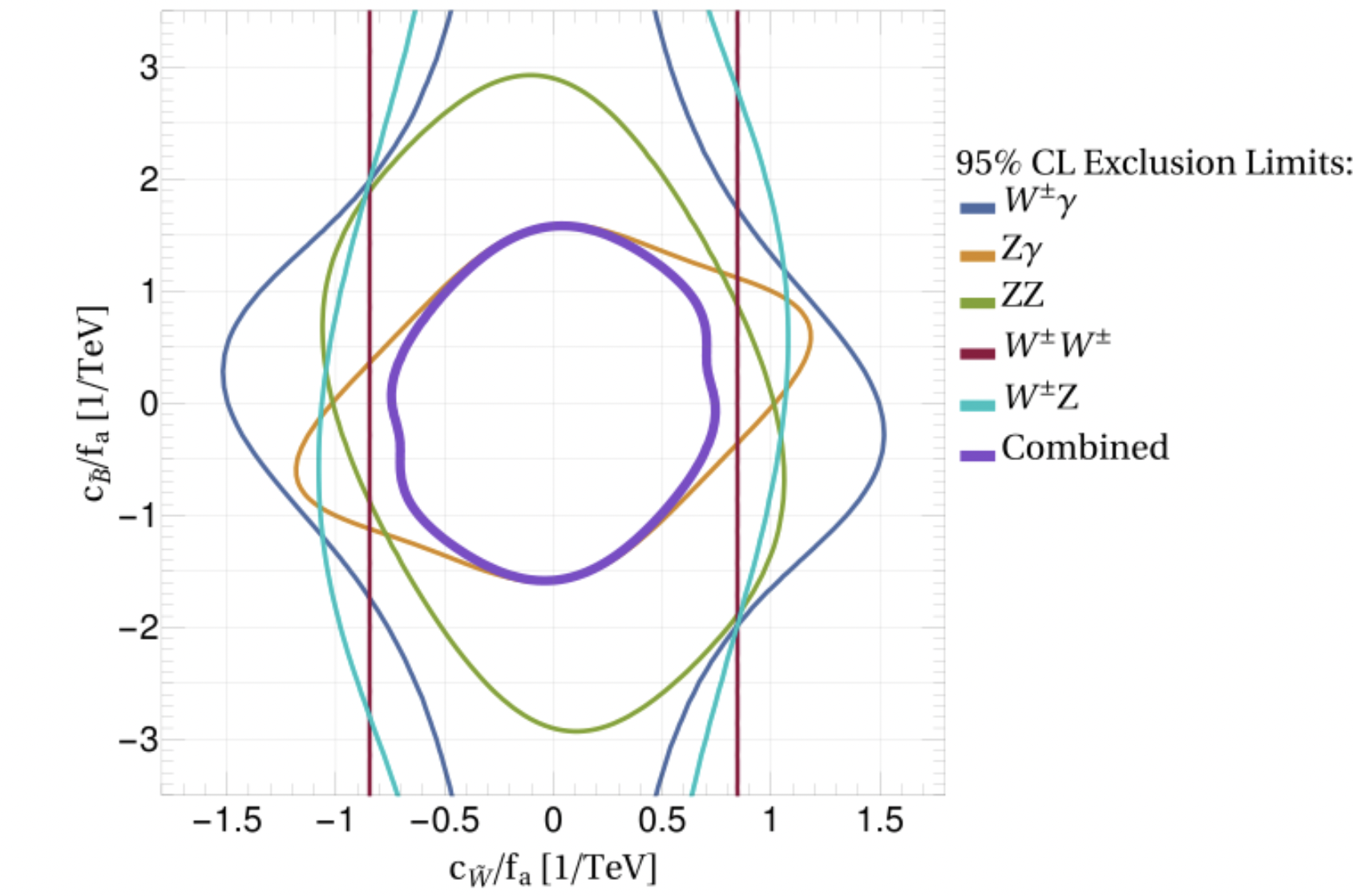
Figure 3. Observed 95% confidence-level exclusion limits in the 2-dimensional space of the ALP couplings to electroweak bosons. The limits are obtained comparing the predicted ALP signal to Run 2 VBS measurements by the CMS Collaboration.

Figure 4 shows the expected limits that can be obtained in the future, performing the same experimental analyses with higher integrated luminosities. The green and orange lines correspond to 300 and 3000 fb^-1 respectively, that are representative of the data sets to be accumulated at the end of the LHC Run 3 and of the HL-LHC. The solid curves contain values of the ALP parameters that will be excluded if the non-observation of signals persists. On the other hand, if a non-resonant signal is detected, the experimental analyses will identify a different preferred region, away from the (0,0) point that represents the SM-only hypothesis. In order to claim the discovery of ALPs through this measurement, the SM point needs to be excluded by at least 5 standard deviations, which can only happen if the signal is strong enough. In Fig. 4, the dashed orange curve labeled as “discovery limit” marks the minimum values of (cW/fa, cB/fa) for which a discovery will be possible by the end of the HL-LHC.

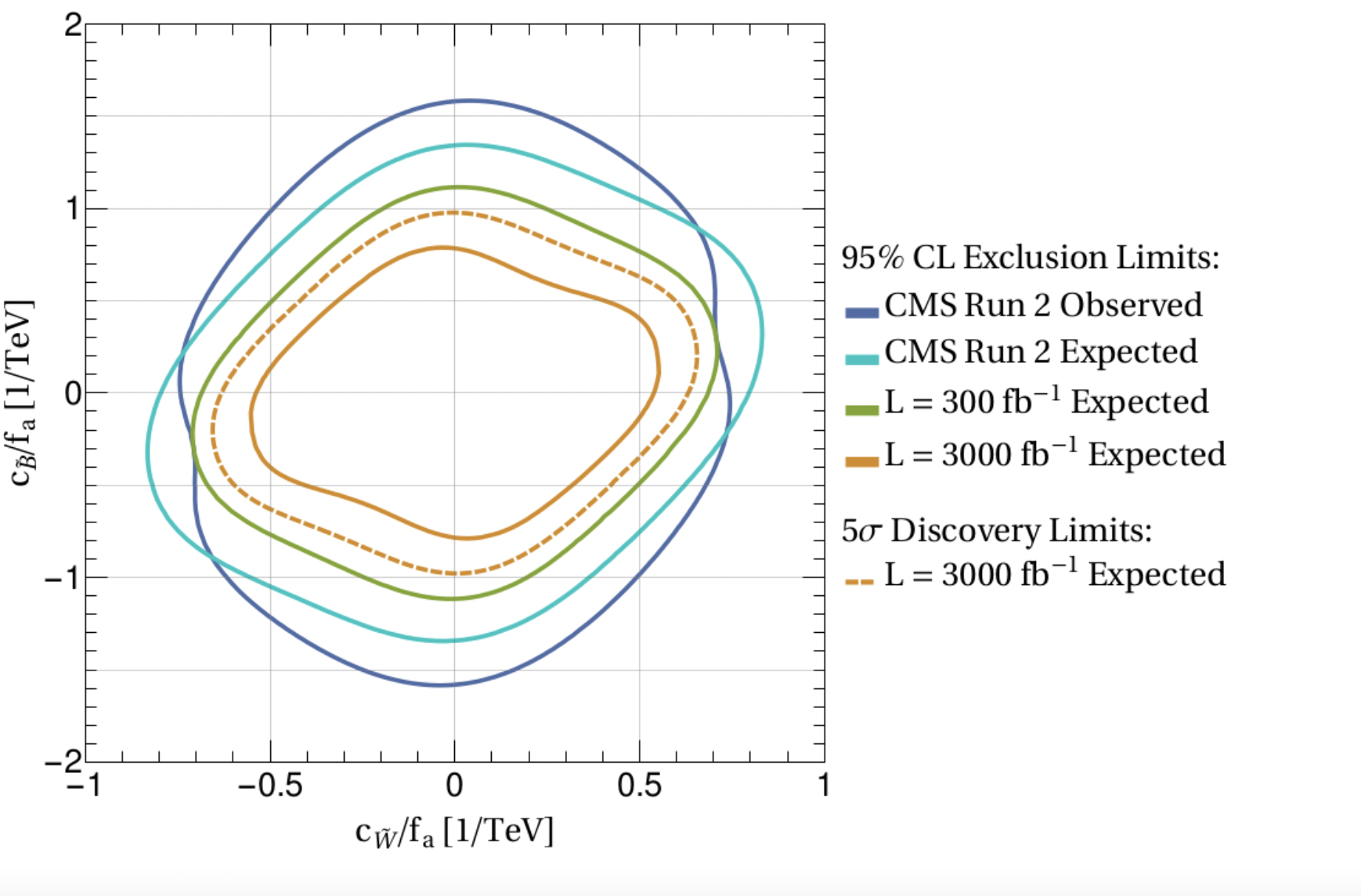
Figure 4. 95% confidence-level expected limits for integrated luminosities attainable at the end of the LHC Run 3 (green) and at the end of the HL-LHC operations (orange), compared to the observed and expected limits from the LHC Run 2 (blue). The dashed orange line marks the “discovery limit” at the HL-LHC: for values of the ALP couplings outside this region, the observation of a non-resonant signal would rule out the pure SM hypothesis at 5 or more standard deviations.

Figure 5 compares the observed Run 2 limits in Figure 3 to other constraints that were previously derived on ALP interactions using different techniques (for further details see [4] and references therein). This comparison is best performed by projecting VBS limits onto the four ALP interactions with electroweak boson pairs (called g_aγγ, ga_WW, g_aZZ, ga_γZ in the Figure) and plotting them as a function of the ALP mass.

In each panel, our result is indicated with a thick, red dashed line and the result from non-resonant searches in diboson (“nonresonant ggF”) with thick, light blue lines. As mentioned above, they hold from arbitrarily low ALP masses up to masses of the order of 100 GeV. Values of the couplings above the line and within the filled regions are currently excluded. The colors highlight the fact that most bounds are derived making explicit assumptions on other ALP couplings. For instance, those marked in dark blue stem from resonant γγ searches at LEP and LHC, and their interpretation requires the coupling to gluons to be much larger than that to photons. The non-resonant constraint from diboson also bears a dependence on the gluon coupling (cG/fa). In the figure they are all shown for a fixed value of (cG/fa), but it’s important to know that for (cG/fa) larger than this baseline, the light blue line moves lower in the plot, for smaller (cG/fa) the line moves higher, and for (cG/fa)=0 these constraints disappear completely. The constraints from non-resonant VBS, on the other hand, are independent of (cG/fa).

Taking into account all these differences we find that, in general, non-resonant constraints are extremely valuable in the hunt for ALPs, because they are sensitive to parameter space regions that are not covered by any other measurement. In particular, in the presence of a large interaction with gluons, non-resonant searches in inclusive diboson are extremely sensitive to ALPs interacting with any diboson pair, to the point that they can be more sensitive than searches for resonant or invisible ALP signals. On the other hand, in scenarios with small ALP-gluon interactions, non-resonant searches in VBS become the main probes for ALP couplings to ZZ and WW pairs at ALP masses above 1 GeV.

Figure 5. Constraints on the ALP couplings to the electroweak bosons obtained from non-resonant searches, compared to limits from other measurements. Those denoted by “Nonresonant ggF” are extracted from non-resonant ALP searches in inclusive diboson production [1,2,3], for a fixed value of the coupling to gluons. The remaining ones are extracted from a variety of other measurements. A more detailed description and all references are provided in [4].

Casting an eye into the future, dedicated analyses at future LHC and HL-LHC Runs might actually achieve sensitivities that exceed our projections. This will depend on several factors that are currently hard to predict, but will likely have a significant impact on the results. Examples are the possibility to optimize the experimental selections, to use finer binnings for the measured distributions, or to incorporate further VBS channels into the analysis (e.g. high-mass γγ or semileptonic final states). All these elements will go in the direction of improving the sensitivity of VBS measurements to non-resonant ALP signals, increasing the chances for a discovery.

From a broader perspective, our results and those of Refs [1,2,3] highlight the potential of non-resonant searches to constrain light new physics and show that they are often complementary to resonant and low-energy searches. This brings a brand new approach to the quest for light new physics that could find broader applications and potentially open new avenues in the future.

REFERENCES

[1] M. Gavela, J. No, V. Sanz and J. F. de Trocóniz, Nonresonant Searches for Axionlike Particles at the LHC, Phys. Rev. Lett. 124 (2020) 051802, [1905.12953]

[2] S. Carrà, V. Goumarre, R. Gupta, S. Heim, B. Heinemann, J. Küchler, F. Meloni, P. Quilez and Y.-C. Yap, Constraining off-shell production of axionlike particles with Zγ and WW differential cross-section measurements, Phys. Rev. D 104 (2021) 092005, [2106.10085]

[3] CMS collaboration, A. Tumasyan et al., Search for heavy resonances decaying to ZZ or ZW and axion-like particles mediating nonresonant ZZ or ZH production at √s = 13 TeV [2111.13669]

[4] J. Bonilla, I. Brivio, J. Machado-Rodríguez and J. F. de Trocóniz, Nonresonant searches for Axion-Like Particles in Vector Boson Scattering Processes at the LHC [2202.03450]

[5] R. Covarelli, M. Pellen and M. Zaro, Vector-Boson scattering at the LHC: Unraveling the electroweak sector, Int. J. Mod. Phys. A 36 (2021) 2130009 [2102.10991]

[6] CMS collaboration, A. M. Sirunyan et al., Measurements of production cross sections of WZ and same-sign WW boson pairs in association with two jets in proton-proton collisions at √s = 13 TeV, Phys. Lett. B 809 (2020) 135710, [2005.01173]

[7] CMS collaboration, A. M. Sirunyan et al., Evidence for electroweak production of four charged leptons and two jets in proton-proton collisions at √s = 13 TeV, Phys. Lett. B 812 (2021) 135992, [2008.07013]

[8] CMS collaboration, A. M. Sirunyan et al., Observation of electroweak production of Wγ with two jets in proton-proton collisions at √s = 13 TeV, Phys. Lett. B 811 (2020) 135988, [2008.10521]

[9] CMS collaboration, A. Tumasyan et al., Measurement of the electroweak production of Zγ and two jets in proton-proton collisions at √s = 13 TeV and constraints on anomalous quartic gauge couplings, Phys. Rev. D 104 (2021) 072001 [2106.11082]